


Next: 5.20 Πέμπτη ομάδα ασκήσεων
Up: 5 Ημερολόγιο διαλέξεων
Previous: 5.18 Υπολογισμοί μέσων τιμών
Contents
Αναφερθήκαμε στην ύπαρξη ροπών ανώτερης τάξης. Λέμε ότι μια ΤΜ 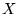 έχει ροπή
τάξης
έχει ροπή
τάξης
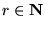 αν
αν
Τότε έπεται ότι έχει και ροπές κάθε μικρότερης τάξης.
Η κεντρική ροπή τάξης 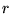 ορίζεται ως η μέση τιμή
ορίζεται ως η μέση τιμή
και υπάρχει όταν υπάρχει ροπή τάξης 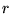 (βλέπε παραπάνω).
(βλέπε παραπάνω).
Η σημαντικότερη περίπτωση είναι η κεντρική ροπή δεύτερης τάξης, η διασπορά
της 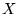 :
:
Είδαμε διάφορες ιδιότητες αυτής της ποσότητας, η πιο σημαντική από τις οποίες
είναι ότι αν 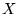 και
και 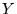 ανεξάρτητες και έχουν ροπή δεύτερης τάξης τότε
ανεξάρτητες και έχουν ροπή δεύτερης τάξης τότε
Η διασπορά (ακριβέστερα, η τετραγωνική της ρίζα
![$\sigma(X) = \sqrt{{{\bf Var}\left[{X}\right]}}$](img83.png) που
ονομάζεται τυπική απόκλιση) αποτελεί ένα μέτρο του πόσο συγκεντρωμένη
είναι η πυκνότητα πιθανότητας της
που
ονομάζεται τυπική απόκλιση) αποτελεί ένα μέτρο του πόσο συγκεντρωμένη
είναι η πυκνότητα πιθανότητας της 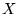 γύρω από τη μέση τιμή της. Για παράδειγμα, το
να έχουμε διασπορά 0 ισοδυναμεί με το να είναι η ΤΜ σταθερή.
γύρω από τη μέση τιμή της. Για παράδειγμα, το
να έχουμε διασπορά 0 ισοδυναμεί με το να είναι η ΤΜ σταθερή.
Είδαμε επίσης τρείς πολύ σημαντικές ανισότητες:
- Ανισότητα Cauchy-Schwartz:
- Ανισότητα Markov: Αν
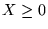
- Ανισότητα Chebyshev:
Οι ανισότητες Markov και Checbyshev έχουν μεγάλη σημασία γιατί δίνουν
ένα άνω φράγμα για την πιθανότητα μια ΤΜ να αποκλίνει από τη μέση τιμή της.
Τέλος ορίσαμε και τη συνδιακύμανση (covariance) δύο ΤΜ 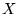 και
και 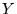
Όταν οι 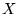 και
και 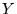 είναι ανεξάρτητες τότε (αλλά όχι μόνο τότε) έχουμε
είναι ανεξάρτητες τότε (αλλά όχι μόνο τότε) έχουμε
![${{\bf Cov}\left[{X,Y}\right]} = 0$](img89.png) . Όταν ισχύει αυτή η τελευταία ισότητα λέμε ότι οι
. Όταν ισχύει αυτή η τελευταία ισότητα λέμε ότι οι 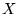 και
και
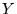 είναι ασυσχέτιστες.
είναι ασυσχέτιστες.
Mihalis Kolountzakis
![]() έχει ροπή
τάξης
έχει ροπή
τάξης
![]() αν
αν
![]() :
:
![]() και
και ![]()