Σεμινάριο Προβλημάτων
- 1 Ωράριο
- 2 Περιγραφή του μαθήματος
- 3 Βαθμολογικό Σύστημα - Συμμετοχή - Εξετάσεις
- 4 Ημερολόγιο Μαθήματος
- 4.1 Τρ, 20-9-2016
- 4.2 Πέ, 22-9-2016
- 4.3 Τρ, 27-9-2016
- 4.4 Πέ, 29-9-2016
- 4.5 Τρ, 4-10-2016
- 4.6 Πέ, 6-10-2016
- 4.7 Τρ, 11-10-2016
- 4.8 Πέ, 13-10-2016
- 4.9 Τρ, 18-10-2016
- 4.10 Πέ, 20-10-2016
- 4.11 Τρ, 25-10-2016
- 4.12 Πέ, 27-10-2016
- 4.13 Τρ, 1-11-2016
- 4.14 Πέ, 3-11-2016
- 4.15 Τρ, 8-11-2016
- 4.16 Πέ, 10-11-2016
- 4.17 Τρ, 22-11-2016
- 4.18 Πέ, 24-11-2016
- 4.19 Τρ, 19-11-2016
- 4.20 Πέ, 1-12-2016
- 4.21 Τρ, 6-12-2016
- 4.22 Πέ, 8-12-2016
- 4.23 Τρ, 13-12-2016
- 4.24 Πέ, 15-12-2016
- 4.25 ΑΝΑΚΟΙΝΩΣΗ: Μάθημα πριν το τελικό διαγώνισμα
- 4.26 ΑΝΑΚΟΙΝΩΣΗ: Τελικό διαγώνισμα και τελικοί βαθμοί
Τρίτη 11-1, Πέμπτη 11-1 στην αίθουσα Ε203.
Δείτε την ανακοίνωση του μαθήματος
εδώ..
Το αντίστοιχο μάθημα το 2013-14 είναι εδώ.
Δεν υπάρχουν προαπαιτούμενα (αλλά δείτε την ανακοίνωση του μαθήματος).
Η συμμετοχή σας στο μάθημα είναι υποχρεωτική. Αυτό δε σημαίνει ότι θα παίρνω απουσίες αλλά
όσοι συμμετέχουν ενεργά στο μάθημα θα παίρνουν, όποτε πουν κάποια καλή ιδέα που μας οδηγεί σε λύση, από ένα πόντο («καραμέλα») ή και
περισσότερους.
Ο βαθμός συμμετοχής σας (Σ) θα είναι το πόσους πόντους μαζέψατε στο εξάμηνο διαιρεμένο από ένα αριθμό που θα καθορίσω στο τέλος ανάλογα
με το πώς έχει πάει το μάθημα.
Αν είναι F ο βαθμός σας στην τελική εξέταση τότε ο βαθμός του μαθήματος θα είναι (F+Σ)/2.
Το ίδιο βαθμολογικό σύστημα θα ισχύσει και στην περίοδο Σεπτεμβρίου και σε κάθε άλλη εξέταση του μαθήματος.
Σκοπός του μαθήματος είναι να καλλιεργήσει στον φοιτητή την ικανότητα να προσεγγίζει νέα και άγνωστα προβλήματα,
και ο τρόπος που θα γίνεται αυτό είναι να ανταλλάσονται ιδέες μέσα στην τάξη με μορφή συζήτησης. Οι πιο πολλές από αυτές τις
ιδέες θα είναι, νομοτελειακά, λανθασμένες ή άκαρπες, αλλά κάποια στιγμή θα μπαίνουμε στο σωστό δρόμο και θα λύνουμε το πρόβλημα.
Γι' αυτό θα πρέπει να είστε μέσα στις συναντήσεις του μαθήματος.
Σήμερα ασχοληθήκαμε με τα παρακάτω προβλήματα:
- Πώς να κρεμάσετε ένα κάδρο από δύο καρφιά
- ΕΡΕΥΝΑ: «Έχετε απατήσει τη/ο σύντροφό σας αυτό το καλοκαίρι;»
- Πώς να γεμίσετε μια κομμένη σκακιέρα με ντόμινα
- Ο συντομότερος δρόμος από ένα σημείο του τοίχου προς ένα σημείο του δαπέδου
- Διχοτόμηση ενός χωραφιού σχήματος Γ
- Τα πολλαπλάσια ενός αρρήτου αριθμού έχουν κλασματικά μέρη πυκνά στο
![$[0,1]$](img1.png) .
.
- Πώς να βρούμε τα κάλπικα νομίσματα
- Πώς να στείλετε ένα κλειδωμένο γράμμα
Μοιράστηκαν 7 καραμέλες σε 4 άτομα συνολικά.
Σήμερα ασχοληθήκαμε με τα παρακάτω προβλήματα:
- Ανακάτεμα τσάι με καφέ.
- Ένα παιχνίδι με τραπουλόχαρτα
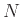 άτομα πάνε σε ένα πάρτυ και ανταλάσσουν χειραψίες μεταξύ τους. Δείξτε ότι υπάρχουν δύο άτομα που αντάλλαξαν τον ίδιο αριθμό χειραψιών.
άτομα πάνε σε ένα πάρτυ και ανταλάσσουν χειραψίες μεταξύ τους. Δείξτε ότι υπάρχουν δύο άτομα που αντάλλαξαν τον ίδιο αριθμό χειραψιών.
- Ένας κυκλικός αυτοκινητόδρομος με βανζινάδικα.
- Πώς να μετρήσετε το χρόνο με δύο φυτίλια.
- Παιχνίδι μ' ένα τόπι.
- Έχουμε μια σκακιέρα
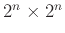 που ένα από τα τετραγωνάκια της λείπει. Δείξτε ότι όπου και να είναι αυτό το τετραγωνάκι
το υπόλοιπο που απομένει μπορεί να "πλακοστρωθεί" με πλακάκια σχήματος L (δηλ. 3 τετραγωνάκια το καθένα).
που ένα από τα τετραγωνάκια της λείπει. Δείξτε ότι όπου και να είναι αυτό το τετραγωνάκι
το υπόλοιπο που απομένει μπορεί να "πλακοστρωθεί" με πλακάκια σχήματος L (δηλ. 3 τετραγωνάκια το καθένα).
Μοιράστηκαν 5 καραμέλες σε 2 άτομα συνολικά.
Σήμερα ασχοληθήκαμε με τα παρακάτω προβλήματα:
- Άθροισμα διαστάσεων ορθογωνίου παραλληλεπιπέδου που περιέχεται σε άλλο τέτοιο
- Δείξαμε ότι η ακολουθία
είναι φραγμένη και συγκλίνει.
- Έχουμε 2 m σχοινί και θέλουμε να πιάσουμε τα δύο άκρα με τα χέρια μας και χωρίς να τα αφήσουμε να πετύχουμε στο τέλος
το σχοινί να δεθεί κόμπο.
- Δύο ίδια νομίσματα είναι τοποθετημένα πάνω σε ένα τραπέζι, το ένα δίπλα στο άλλο (ακουμπάνε). Κρατάμε το αριστερό νόμισμα
σταθερό και το δεξί νόμισμα γυρνάει γύρω από το αριστερό κυλώντας πάνω του (χωρίς να γλυστράει) μέχρι να ξαναγυρίσει στη
θέση του. Πόσες περιστροφές γύρω από τον εαυτό του έχει κάνει το δεξί νόμισμα;
- A New York story. A young man lives in Manhattan near a subway station. He has two girl friends, one in Brooklyn, one in The Bronx. To visit the girl in Brooklyn he takes a train on one side of the platform; to visit the girl in The Bronx he takes a train on the other side of the same platform. Since he likes both girls equally well, he simply takes the first train that comes along. The young man reaches the subway platform at a random moment each Saturday afternoon. Brooklyn and Bronx trains run every 10 minutes. For some reason he finds himself spending most of his time with the girl in Brooklyn: in fact on the average he goes there nine times out of ten. Why does this happen?
- Έχουμε τυλίξει ένα σχοινί γύρω από τον ισημερινό της γης, σφιχτά ώστε το σχοινί να είναι ακριβώς πάνω στο έδαφος (υποθέτουμε ότι η γη είναι μια τέλεια σφαίρα).
Κόβουμε το σχοινί σε ένα σημείο και προσθέτουμε ένα μέτρο στο μήκος του. Στη συνέχεια ανυψώνουμε το σχοινί αυτό πάνω από τον ισημερινό, κατά
το ίδιο μήκος παντού, ώστε να είναι και πάλι τεντωμένο. Κατά πόσο σηκώθηκε;
- Δύο αυτοκίνητα που είναι 100 χλμ μακριά το ένα από το άλλο αρχίζουν να κινούνται το ένα προς το άλλο (βρίσκονται πάνω σε μια ευθεία) το αριστερό αυτοκίνητο με 20 χλμ/ώρα και το δεξί με 30 χλμ/ώρα. Πάνω στο δεξί αυτοκίνητα λιάζεται μια μύγα που τρομάζει όταν ξεκινάει το αυτοκίνητο και αρχίζει να κινείται προς τα αριστερά με ταχύτητα 40 χλμ/ώρα. Κάποια στιγμή προσκρούει στο αριστερό αυτοκίνητο και αρχίζει να κινείται προς τα δεξιά με την ίδια ταχύτητα. Όταν προσκρούσει ξανά στο δεξί αυτοκίνητο αντιστρέφει και πάλι τη φορά της κίνησής της, κ.ο.κ, μέχρις να συνθλιβεί ανάμεσα στα δύο αυτοκίνητα. Τι απόσταση κάλυψε συνολικά η μύγα μέχρι το τέλος της;
- Έστω
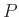 ένα πολύεδρο στο
ένα πολύεδρο στο
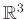 . Δείξτε ότι έχει δύο έδρες με τον ίδιο αριθμό ακμών.
. Δείξτε ότι έχει δύο έδρες με τον ίδιο αριθμό ακμών.
- Ένα περίεργο πρόβλημα (που κατά τον V. I. Arnold
οι Αμερικάνοι μαθητές το λύνουν αμέσως αλλά οι Ρώσοι «κολλάνε»):
έχουμε ένα ορθογώνιο τρίγωνο με υποτείνουσα 10m και με ύψος προς την υποτείνουσα 6m. Ποιο είναι το εμβαδό του;
Μοιράστηκαν 2 καραμέλες σε 2 άτομα συνολικά.
Σήμερα ασχοληθήκαμε με τα παρακάτω προβλήματα:
- Μια ορθογώνια σοκολάτα
- Τα τρία κουτιά με τη λίρα
Στην ίδια συζήτηση δείτε και το πρόβλημα στο σχόλιο 2 το οποίο επίσης συζητήσαμε.
- Πώς μπορεί κανείς να βρει μια φόρμουλα για την απόλυτη τιμή του
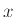 αν μπορεί να χρησιμοποιήσει τη συνάρτηση
αν μπορεί να χρησιμοποιήσει τη συνάρτηση
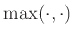 . Αντίστροφα, πώς μπορεί κανείς να γράψει μια φόρμουλα για τη συνάρτηση
. Αντίστροφα, πώς μπορεί κανείς να γράψει μια φόρμουλα για τη συνάρτηση 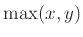 αν μπορεί
να χρησιμοποιήσει τη συνάρτηση της απόλυτης τιμής.
αν μπορεί
να χρησιμοποιήσει τη συνάρτηση της απόλυτης τιμής.
- Κάθε φυσικός αριθμός
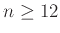 μπορεί να γραφεί ως γραμμικός συνδυασμός του 4 και του 5 με μη αρνητικούς ακέραιους συντελεστές.
μπορεί να γραφεί ως γραμμικός συνδυασμός του 4 και του 5 με μη αρνητικούς ακέραιους συντελεστές.
- Έχουμε
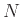 πόλεις, κάθε δύο από τις οποίες ενώνονται μεταξύ τους με έναν απ' ευθείας μονόδρομο. Δείξτε ότι όποιες και
να είναι οι κατευθύνσεις αυτών των μονόδρομων πάντα υπάρχει τρόπος να κινηθούμε πάνω σε αυτό το δίκτυο δρόμων ώστε να περάσουμε
ακριβώς μια φορά από κάθε πόλη.
πόλεις, κάθε δύο από τις οποίες ενώνονται μεταξύ τους με έναν απ' ευθείας μονόδρομο. Δείξτε ότι όποιες και
να είναι οι κατευθύνσεις αυτών των μονόδρομων πάντα υπάρχει τρόπος να κινηθούμε πάνω σε αυτό το δίκτυο δρόμων ώστε να περάσουμε
ακριβώς μια φορά από κάθε πόλη.
Αυτό το πρόβλημα δεν το λύσαμε μέσα στην τάξη. Οι φοιτητές θα πρέπει να το σκεφτούν μόνοι τους και θα το συζητήσουμε την επόμενη φορά.
- Το παράδοξο του διαγνωστικού τεστ
Μοιράστηκαν 3 καραμέλες σε 3 άτομα συνολικά.
Σήμερα ασχοληθήκαμε με τα παρακάτω προβλήματα:
- Διακόπτες και λάμπες
- Πώς να εξαφανίσετε ένα σημείο από τον κύκλο
- Προς τα πού πήγε το ποδήλατο;
- Ο αποτελεσματικός ηλεκτρολόγος
- Οι 7 ληστές
Δόθηκαν 6 καραμέλες σε 6 άτομα.
Σήμερα ασχοληθήκαμε με τα παρακάτω προβλήματα:
- Μια στήλη από τούβλα
- Νομίσματα πάνω σ’ ένα τραπέζι
- Με πόσους τρόπους μπορούμε να επιλέξουμε δύο ξένα μεταξύ τους υποσύνολα
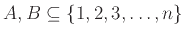 ;
;
- Αν
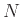 σημεία
σημεία
![$x_1, x_2, \ldots, x_N \in [0,1]^2$](img12.png) είναι τέτοια ώστε για κάθε σημείο
είναι τέτοια ώστε για κάθε σημείο ![$x \in [0,1]^2$](img13.png) υπάρχει κάποιο
υπάρχει κάποιο
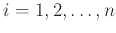 με
με
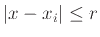 τότε δείξτε ότι
τότε δείξτε ότι
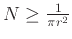 .
.
Δόθηκαν 4 καραμέλες σε 4 άτομα.
Σήμερα ασχοληθήκαμε με τα παρακάτω προβλήματα:
- Αποδείξαμε ότι δεν υπάρχει ακολουθία αριθμών
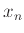 που στις τιμές της να συμπεριλαμβάνονται όλοι
οι αριθμοί στο διάστημα
που στις τιμές της να συμπεριλαμβάνονται όλοι
οι αριθμοί στο διάστημα 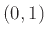 . Με άλλα λόγια δείξαμε ότι το σύνολο των πραγματικών αριθμών
δεν είναι αριθμήσιμο, είναι, όπως λέμε, υπεραριθμήσιμο. Ορίσαμε τι είναι αλγεβρικοί αριθμοί
και αποδείξαμε ότι το πλήθος των αλγεβρικών αριθμών είναι αριθμήσιμο άρα υπάρχουν πραγματικοί αριθμοί
που δεν είναι αλγεβρικοί. Ομοίως ορίσαμε τι σημαίνει μια υπολογίσιμη συνάρτηση
. Με άλλα λόγια δείξαμε ότι το σύνολο των πραγματικών αριθμών
δεν είναι αριθμήσιμο, είναι, όπως λέμε, υπεραριθμήσιμο. Ορίσαμε τι είναι αλγεβρικοί αριθμοί
και αποδείξαμε ότι το πλήθος των αλγεβρικών αριθμών είναι αριθμήσιμο άρα υπάρχουν πραγματικοί αριθμοί
που δεν είναι αλγεβρικοί. Ομοίως ορίσαμε τι σημαίνει μια υπολογίσιμη συνάρτηση
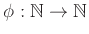 και
αποδείξαμε ότι το πλήθος των υπολογισίμων συναρτήσεων, που είναι το πολύ το πλήθος των προγραμμάτων
που υπάρχουν, είναι αριθμήσιμο. Αφού το πλήθος των συναρτήσεων είναι υπεραριθμήσιμο έπεται
οτι υπάρχουν συναρτήσεις που δεν είναι υπολογίσιμες.
και
αποδείξαμε ότι το πλήθος των υπολογισίμων συναρτήσεων, που είναι το πολύ το πλήθος των προγραμμάτων
που υπάρχουν, είναι αριθμήσιμο. Αφού το πλήθος των συναρτήσεων είναι υπεραριθμήσιμο έπεται
οτι υπάρχουν συναρτήσεις που δεν είναι υπολογίσιμες.
Αν σας ενδιαφέρει μπορείτε να διαβάσετε μερικά παραπάνω πράγματα γι' αυτές τις έννοιες
στο βιβλίο αυτό, §1.8 και Κεφ. 10.
- Έχουμε 100 κουτιά κλειστά στη σειρά. Περνάει το πρώτο άτομο και τα ανοίγει όλα. Περνάει το 2ο και κλείνει κάθε 2ο κουτί (πολλαπλάσιο του 2),
περνάει ο 3ος και αλλάζει την κατάσταση κάθε 3ου κουτιού (πολλαπλάσια του 3), κλπ. Αφού περάσουν 100 άτομα, ποια κουτιά είναι ανοιχτά;
- Κόψαμε ένα στρογγυλό κέικ σε τρία ίδια κομμάτια με τρεις ευθείς κοπές.
- Ξεκινήσαμε να αποδείξουμε το παρακάτω θεώρημα: κάθε δύο ισεμβαδικά πολύγωνο στο επίπεδο μπορούν να κοπούν σε πεπερασμένα κομμάτια
το καθένα ώστε συνολικά τα κομμάτια αυτά να είναι ίδια. Ισοδύναμε, μπορούμε να κόψουμε το ένα πολύγωνο σε πεπερασμένα στο πλήθος
κομμάτια και να πάρουμε το άλλο πολύγωνο συναρμολογώντας τα διαφορετικά. Δείξαμε κατ' αρχήν ότι μπορούμε να κόψουμε
ένα τρίγωνο και να φτιάξουμε ένα παραλληλόγραμο, ένα παραλληλόγραμμο και να φτιάξουμε ένα ορθογώνιο και τέλος (μετά πολλών
βασάνων) δείξαμε ότι κάθε ορθογώνιο μπορεί να κοπεί σε κομμάτια ώστε να φτιάξουμε ένα τετράγωνο. Θα τελειώσουμε την απόδειξη την Πέμπτη.
Δόθηκαν 6 καραμέλες σε 5 άτομα.
Σήμερα ασχοληθήκαμε με τα παρακάτω προβλήματα:
- Τελειώσαμε το πρόβλημα που είχαμε ξεκινήσει την προηγούμενη φορά και στο οποίο δείξαμε ότι οποιαδήποτε δύο πολύγωνα ίσου
εμβαδού μπορούν να τεμαχιστούν σε πεπερασμένα πλήθος από (πολυγωνικά) κομμάτια τα οποία ανά δύο να είναι ίσα.
Ένας άλλος τρόπος να δει κανείς το ίδιο πρόβλημα είναι να πει ότι μπορούμε να κόψουμε το πρώτο πολύγωνο σε κομμάτια και
να φτιάξουμε το άλλο συναρμολογώντας τα διαφορετικά.
- Έχουμε 100 νομίσματα, διαφόρων αξιών, τοποθετημένα σε μια σειρά πάνω σε ένα τραπέζι. Δύο παίχτες εναλλάσονται και παίρνουν ο καθένας ένα
από τα δύο νομίσματα που είναι στις δύο άκρες της σειράς. Κερδίζει όποιος παίχτης πάρει συνολικά τη μεγαλύτερη αξία.
Πώς πρέπει να παίξει ο πρώτος παίκτης ώστε να κερδίσει (ακριβέστερα, ώστε να μη χάσει αφού υπάρχει περίπτωση να παίρνουν και οι δύο το ίδιο
ποσό, όπως όταν όλες οι αξίες των νομισμάτων είναι ίσες);
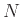 άτομα κάθονται γύρω από ένα στρογγυλό τραπέζι και θέλουν να υπολογίσουν το άθροισμα των μισθών τους χωρίς όμως να αποκαλύψουν ο ένας
στον άλλο καμιά πληροφορία για το δικό τους μισθό. Είδαμε διάφορους τρόπους με τους οποίους μπορεί να γίνει αυτό.
άτομα κάθονται γύρω από ένα στρογγυλό τραπέζι και θέλουν να υπολογίσουν το άθροισμα των μισθών τους χωρίς όμως να αποκαλύψουν ο ένας
στον άλλο καμιά πληροφορία για το δικό τους μισθό. Είδαμε διάφορους τρόπους με τους οποίους μπορεί να γίνει αυτό.
- Περιττό πλήθος στρατιωτών στο επίπεδο βρίσκονται όλοι σε διαφορετικές αποστάσεις μεταξύ τους. Ο καθένας τους έχει εντολή να κοιτάει τον
πλησιέστερο στρατιώτη σε αυτόν. Δείξτε ότι υπάρχει κάποιος στρατιώτης που δεν τον κοιτάει κανείς.
- Σε ένα τελωνείο φτάνει ένα έγγραφο που ζητά να γίνονται τυχαίοι έλεγχοι στα εισερχόμενα για τυχόν απαγορευμένα εμπορεύματα.
Για λόγους νομικούς η διοίκηση ζητά να κρατούνται για έλεγχο κάθε μέρα «100 αντικείμενα επιλεγμένα απολύτως τυχαία από τα αντικείμενα της ημέρας«.
Ο διευθυντής του τελωνείου είναι πολύ προβληματισμένος αφού δεν ξέρει πώς να επιλέξει αυτά τα 100 αντικείμενα τυχαία
χωρίς να περιμένει να μπουν μέσα όλα τα εμπορεύματα της ημέρας.
Αν ήξερε στην αρχή της ημέρας πόσα αντικείμενα θα μπουν θα μπορούσε να κάνει την τυχαία επιλογή του το πρωί,
και να ξέρει ποια αντικείμενα θα πρέπει να κρατήσει για έλεγχο και ποια να διεκπεραιώσει αμέσως.
Όμως δεν ξέρει. Κατά τη διάρκεια της ημέρας φθάνουν αντικείμενα για επεξεργασία στην υπηρεσία του απροειδοποίητα και
δεν έχει χώρο να κρατήσει πάνω από 100 αντικείμενα στην αποθήκη του. Τι θα πρέπει να κάνει;
Το ξεκινήσαμε αυτό το πρόβλημα αλλά δεν το τελειώσαμε. Θα το κάνουμε την επόμενη φορά.
Δόθηκαν 4 καραμέλες σε 4 άτομα.
Σήμερα ασχοληθήκαμε με τα παρακάτω προβλήματα:
- Τελωνειακός Έλεγχος: Τελειώσαμε αυτό το πρόβλημα που είχαμε
ξεκινήσει την προηγούμενη φορά.
- Το πέμπτο χαρτί
- Τραπουλόχαρτα σε σωρούς. Για το πρόβλημα αυτό
αναφέραμε και το «Θεώρημα του Γάμου» για το οποίο ίσως να πούμε κι άλλα την επόμενη φορά.
Δόθηκαν 2 καραμέλες σε 2 άτομα.
Σήμερα ασχοληθήκαμε με τα παρακάτω προβλήματα:
- Ασχοληθήκαμε με μια παραλλαγή του θεωρήματος του Γάμου, που είχαμε δει την προηγούμενη φορά, και την αποδείξαμε
βασιζόμενοι στο θεώρημα του Γάμου.
- Πτώση μέχρι καταστροφής
- Συνδέσεις
Δόθηκαν 4 καραμέλες σε 4 άτομα.
Σήμερα ασχοληθήκαμε με τα παρακάτω προβλήματα:
- Το τραπέζι του μπιλιάρδου
- Πόσους ελέγχους;
- Αποδείξτε ότι υπάρχουν οσοδήποτε μεγάλα διαστήματα ακεραίων χωρίς πρώτους αριθμούς.
Σήμερα ασχοληθήκαμε με τα παρακάτω προβλήματα:
- Σημεία και χρώματα
- Ανασχηματισμός και οικονομία
- Ισόπλευρα τρίγωνα
Δόθηκαν 3 καραμέλες σε 2 άτομα.
Σήμερα ασχοληθήκαμε με τα παρακάτω προβλήματα:
- Δε γίνεται να πλακοστρώσουμε μια 8x8 σκακιέρα με 1x2 ντόμινα χωρίς δύο από αυτά να σχηματίζουν ένα 2x2 τετράγωνο.
- Για ποιες τιμές του
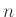 μπορεί ένα τετράγωνο να χωριστεί σε
μπορεί ένα τετράγωνο να χωριστεί σε 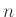 τετράγωνα;
τετράγωνα;
- Πότε μπορεί ένα γράφημα (σχήμα με γραμμές) να σχεδιαστεί μονοκοντυλιά; Αυτό είναι το πρόβλημα της ύπαρξης μονοπατιού ή κυκλώματος Euler σε ένα γράφημα
για το οποίο μπορεί να διαβάσετε π.χ. από εδώ.
Δόθηκαν 4 καραμέλες σε 3 άτομα.
Σήμερα ασχοληθήκαμε με τα παρακάτω προβλήματα:
- Έχουμε
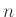 κουτιά τοποθετημένα σε ένα κύκλο. Αρχικά κάθε κουτί περιέχει ένα βώλο και σκοπός μας είναι να μαζέψουμε όλους
τους βώλους σε ένα κουτί. Η μόνη πράξη που μας επιτρέπεται να κάνουμε σε κάθε βήμα είναι να επιλέξουμε δύο βώλους και καθέναν από
αυτούς να τον μετακινήσουμε στο κουτί που είναι αριστερά του ή στο κουτί που είναι δεξιά του. Για ποια
κουτιά τοποθετημένα σε ένα κύκλο. Αρχικά κάθε κουτί περιέχει ένα βώλο και σκοπός μας είναι να μαζέψουμε όλους
τους βώλους σε ένα κουτί. Η μόνη πράξη που μας επιτρέπεται να κάνουμε σε κάθε βήμα είναι να επιλέξουμε δύο βώλους και καθέναν από
αυτούς να τον μετακινήσουμε στο κουτί που είναι αριστερά του ή στο κουτί που είναι δεξιά του. Για ποια 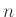 έχει λύση το πρόβλημα;
έχει λύση το πρόβλημα;
- Ποιο είναι το άθροισμα των ψηφίων όλων των φυσικών αριθμών από 1 έως
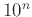 ;
;
- Σε μια ορθογώνια
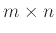 σκακιέρα υπάρχει σε κάποια κελιά από ένα νόμισμα. Στο πάνω αριστερά κελί της σκακιέρας βρίσκεται ένα
robot το οποίο μπορεί να κινείται προς τα δεξιά και κάτω (αλλά όχι προς τα αριστερά ή πάνω). Πώς πρέπει να κινηθεί το robot
ώστε να καταλήξει στο κάτω δεξιά κελί και να μαζέψει από τα κελιά απ' όπου θα περάσει τα περισσότερα νομίσματα;
σκακιέρα υπάρχει σε κάποια κελιά από ένα νόμισμα. Στο πάνω αριστερά κελί της σκακιέρας βρίσκεται ένα
robot το οποίο μπορεί να κινείται προς τα δεξιά και κάτω (αλλά όχι προς τα αριστερά ή πάνω). Πώς πρέπει να κινηθεί το robot
ώστε να καταλήξει στο κάτω δεξιά κελί και να μαζέψει από τα κελιά απ' όπου θα περάσει τα περισσότερα νομίσματα;
Σήμερα ασχοληθήκαμε με τα παρακάτω προβλήματα:
- Υπουργικό Συμβούλιο
- Πώς να πλακοστρώσουμε (tiling) μια
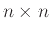 σκακιέρα με ένα πλακάκι 1x1 και πολλά πλακάκια 1x3.
σκακιέρα με ένα πλακάκι 1x1 και πολλά πλακάκια 1x3.
- Έχουμε εκατό νομίσματα σε μια σειρά. Άλλα δείχνουν κορώνα κι άλλα γράμματα. Σε κάθε βήμα μπορούμε να επιλέγουμε ένα διάστημα από αυτά (ακόμη
και με ένα μόνο νόμισμα μέσα) και να τα αναποδογυρίζουμε όλα. Να βρεθεί μια μέθοδος που στη χειρότερη περίπτωση να κάνει όσο γίνεται λιγότερα βήματα και
στο τέλος να αφήνει όλα τα νομίσματα να δείχνουν κορώνα.
Σήμερα ασχοληθήκαμε με τα παρακάτω προβλήματα:
- Πότε μπορούμε να πλακοστρώσουμε μια
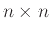 σκακιέρα με πλακάκια 1x2 και 2x1 ώστε να χρησιμοποιηθεί ίδιος αριθμός
από κάθε ένα από τα δύο είδη πλακακιού.
σκακιέρα με πλακάκια 1x2 και 2x1 ώστε να χρησιμοποιηθεί ίδιος αριθμός
από κάθε ένα από τα δύο είδη πλακακιού.
- Ένας πίνακας από κάρτες έχει όλες τις κάρτες να αναφέρουν στην κάτω τους μεριά (που δε φαίνεται) ένα αριθμό. Ο πίνακας είναι 10x10.
Κάθε γραμμή του πίνακα είναι αύξουσα προς τα δεξιά και κάθε στήλη αύξουσα προς τα κάτω. Αν ψάχνουμε να βρούμε τη θέση ενός αριθμού στον
πίνακα να βρεθεί μια μέθοδος που δε χρειάζεται να εξετάσει πάνω από 20 κάρτες μέχρι να βρει τον αριθμό ή να αποφανθεί ότι
ο αριθμός δε βρίσκεται στον πίνακα.
- Σε ένα νησί υπάρχουν
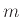 χαμαιλέοντες καφέ χρώματος,
χαμαιλέοντες καφέ χρώματος, 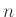 χαμαιλέοντες γκρί χρώματος και
χαμαιλέοντες γκρί χρώματος και 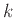 χαμαιλέοντες μαύρου χρώματος.
Όταν συναντηθούν δύο ετερόχρωμοι χαμαιλέοντες τότε παίρνουν κι οι δύο το τρίτο χρώμα. Για ποιες τιμές των
χαμαιλέοντες μαύρου χρώματος.
Όταν συναντηθούν δύο ετερόχρωμοι χαμαιλέοντες τότε παίρνουν κι οι δύο το τρίτο χρώμα. Για ποιες τιμές των 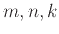 είναι δυνατόν,
μετά από κατάλληλες συναντήσεις, να μετατραπούν όλοι οι χαμαιλέοντες στο ίδιο χρώμα;
είναι δυνατόν,
μετά από κατάλληλες συναντήσεις, να μετατραπούν όλοι οι χαμαιλέοντες στο ίδιο χρώμα;
- Φτιάξαμε μια συνάρτηση
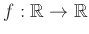 που δεν είναι συνεχής πουθενά, μια συνάρτηση που είναι συνεχής ακριβώς σε ένα σημείο, μια που
είναι συνεχής μόνο σε ένα δεδομένο πεπερασμένο σύνολο σημείων, και μια που είναι συνεχής ακριβώς στους αριθμούς
που δεν είναι συνεχής πουθενά, μια συνάρτηση που είναι συνεχής ακριβώς σε ένα σημείο, μια που
είναι συνεχής μόνο σε ένα δεδομένο πεπερασμένο σύνολο σημείων, και μια που είναι συνεχής ακριβώς στους αριθμούς
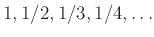 .
.
Δόθηκαν δύο καραμέλες.
Την Πέμπτη 17-11-2016 δε θα γίνει μάθημα λόγω της αργίας του Πολυτεχνείου. Την Τρίτη 15-11-2016 επίσης δε θα γίνει μάθημα λόγω απουσίας δικιάς
μου. Το μάθημα θα αναπληρωθεί αργότερα, πιθανότατα μετά τα Χριστούγεννα.
Σήμερα ασχοληθήκαμε με τα παρακάτω προβλήματα:
- Να κατασκευαστεί μια ακολουθία συναρτήσεων
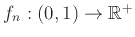 τέτοια ώστε (α) για κάθε
τέτοια ώστε (α) για κάθε 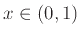 να ισχύει
να ισχύει
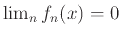 και (β) να ισχύει
και (β) να ισχύει
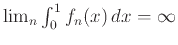 .
.
- Όπως το 1 αλλά με την επιπλέον προϋπόθεση οι
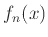 να είναι συνεχείς. Επίσης με το διάστημα
να είναι συνεχείς. Επίσης με το διάστημα ![$[0,1]$](img1.png) στη θέση του
στη θέση του 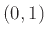 ως πεδίο
ορισμού.
ως πεδίο
ορισμού.
- Να κατασκευαστεί μια ακολουθία συναρτήσεων
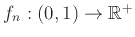 τέτοια ώστε για κάθε
τέτοια ώστε για κάθε 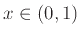 να ισχύει
να ισχύει
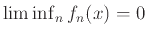 και
και
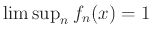 .
.
- Όπως το 3 αλλά με την επιπλέον προϋπόθεση
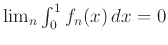 .
.
- Όπως το 3 αλλά με την επιπλέον προϋπόθεση
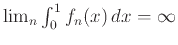 .
.
Δόθηκαν 3 καραμέλες σε 3 άτομα.
Σήμερα συνεχίσαμε σε προβλήματα παρόμοια με αυτά της Τρίτης. Ειδικότερα κατασκευάσαμε διάφορες ακολουθίες συναρτήσεων 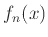 με
ζητούμενες ιδιότητες σύγκλισης (π.χ. κατά σημείο και όχι ομοιόμορφα).
με
ζητούμενες ιδιότητες σύγκλισης (π.χ. κατά σημείο και όχι ομοιόμορφα).
Σήμερα είδαμε το πώς μπορούμε να βρούμε ένα πολυώνυμο 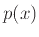 , βαθμού το πολύ
, βαθμού το πολύ 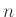 , το οποίο να παίρνει τη δεδομένη τιμή
, το οποίο να παίρνει τη δεδομένη τιμή 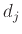 στο σημείο
στο σημείο 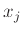 ,
για
,
για
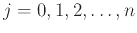 . (Τα σημεία
. (Τα σημεία 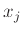 υποτίθενται διαφορετικά ανά δύο.) Είδαμε πώς να το κάνουμε αυτό με γραμμική άλγεβρα αλλά και τα
πολυώνυμα Lagrange που δίνουν μια γρήγορη λύση σε αυτό το πρόβλημα.
υποτίθενται διαφορετικά ανά δύο.) Είδαμε πώς να το κάνουμε αυτό με γραμμική άλγεβρα αλλά και τα
πολυώνυμα Lagrange που δίνουν μια γρήγορη λύση σε αυτό το πρόβλημα.
Είδαμε το λεγόμενο σχήμα του Hornet, που μας επιτρέπει να υπολογίσουμε ένα πολυώνυμο βαθμού 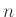 σε ένα σημείο
σε ένα σημείο 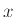 κάνοντας μόνο
κάνοντας μόνο 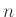 πολλαπλασιασμούς
και
πολλαπλασιασμούς
και 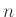 προσθέσεις (εξοικονομώντας έτσι περίπου τους μισούς πολλαπλασιασμούς από τον υπολογισμό με την προφανή μέθοδο που προκύπτει από
τηα γραφή του πολυωνύμου ως άθροισμα μονονύμων).
προσθέσεις (εξοικονομώντας έτσι περίπου τους μισούς πολλαπλασιασμούς από τον υπολογισμό με την προφανή μέθοδο που προκύπτει από
τηα γραφή του πολυωνύμου ως άθροισμα μονονύμων).
Είδαμε πώς μπορούμε να βρούμε ένα πολυώνυμο που σε ένα σημείο έχει δοσμένες τιμές των παραγώγων του.
Αποδείξαμε ότι κάθε πολυώνυμο μιας μεταβλητής που είναι πάντα θετικό στην πραγματικότητα είναι πάντα μεγαλύτερο από κάποιο αριθμό 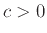 (και δε μπορεί δηλ. να πάρει οσοδήποτε μικρές θετικές τιμές). Πήραμε ως πρόβλημα στο σπίτι το να βρούμε ένα πολυώνυμο
(και δε μπορεί δηλ. να πάρει οσοδήποτε μικρές θετικές τιμές). Πήραμε ως πρόβλημα στο σπίτι το να βρούμε ένα πολυώνυμο 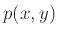 δύο πραγματικών
μεταβλητών που είναι μεν πάντα θετικό αλλά μπορεί να πάρει οσοδήποτε μικρές θετικές τιμές.
δύο πραγματικών
μεταβλητών που είναι μεν πάντα θετικό αλλά μπορεί να πάρει οσοδήποτε μικρές θετικές τιμές.
Δόθηκε μια καραμέλα.
Δείξαμε σήμερα πρώτα ότι υπάρχει ένα πολυώνυμο 2 μεταβλητών, 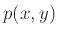 , τέτοιο ώστε (α)
, τέτοιο ώστε (α)
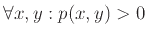 , αλλά και
(β)
, αλλά και
(β)
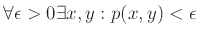 Με άλλα λόγια το πολυώνυμο
Με άλλα λόγια το πολυώνυμο 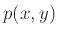 είναι μεν πάντα θετικό αλλά μπορεί
να πάρει οσοδήποτε μικρές τιμές. Αυτό το φαινόμενο δε μπορεί να υπάρξει με πολυώνυμα μιας μεταβλητής. Αν ένα πολυώνυμο
είναι μεν πάντα θετικό αλλά μπορεί
να πάρει οσοδήποτε μικρές τιμές. Αυτό το φαινόμενο δε μπορεί να υπάρξει με πολυώνυμα μιας μεταβλητής. Αν ένα πολυώνυμο 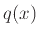 είναι πάντα θετικό τότε υπάρχει μια θετική σταθερά
είναι πάντα θετικό τότε υπάρχει μια θετική σταθερά 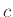 τέτοια ώστε
τέτοια ώστε
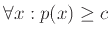 .
Ένα πολυώνυμο που έχει αυτές τις ιδιότητες είναι π.χ. το
.
Ένα πολυώνυμο που έχει αυτές τις ιδιότητες είναι π.χ. το
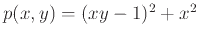 .
.
Έπειτα λύσαμε διάφορα προβλήματα συνδυαστικής. Από το βιβλίο που βρίσκεται εδώ
λύσαμε τις ασκήσεις 3.8, 3.14, 3.17, 3.18, 3.19, 3.21, 3.25.
Δόθηκαν 2 καραμέλες.
Σήμερα συνεχίσαμε να λύνουμε ασκήσεις συνδυαστικής (μέτρημα) όπως και την Τρίτη.
Σήμερα συνεχίσαμε να λύνουμε ασκήσεις συνδυαστικής (μέτρημα) όπως και την Τρίτη.
Σήμερα συνεχίσαμε να λύνουμε ασκήσεις συνδυαστικής (μέτρημα) όπως και την Τρίτη.
Από το βιβλίο που βρίσκεται εδώ
έχουμε καλύψει σχεδόν ολόκληρα
τα κεφάλαι 3 και 4 (Βασικές αρχές απαρίθμησης, Προχωρημένη απαρίθμηση).
Για να προετοιμαστείτε για τις εξετάσεις κοιτάξτε ξανά όλα τα προβλήματα που λύσαμε στο μάθημα
κατά τη διάρκεια του εξαμήνου. Για πολλά από αυτά υπάρχουν δείκτες σε σημείο στο διαδίκτυο όπου θα βρείτε τη λύση (ή μία λύση),
αλλά για αρκετά δεν υπάρχει. Εκεί να συμβουλευτείτε τις σημειώσεις σας. Ολόκληρο το μήνα του Ιανουαρίου θα είμαι διαθέσιμος
στο γραφείο μου για να συζητήσουμε όποιο πρόβλημα δεν καταλαβαίνετε πώς λύνεται.
Καλές διακοπές και καλό διάβασμα.
Το τελικό διαγώνισμα είναι τη Δευτέρα 23-1-2017, 5-8, στην Α208.
Θα κάνουμε ένα δίωρο μαθήματος την προηγούμενη Παρασκευή, 20-1-2017, 1-3μμ, στην αίθουσα όπου γινόταν το μάθημα κατά διάρκεια του εξαμήνου (Ε203).
Δε θα λύσουμε καινούργια προβλήματα. Ο σκοπός του μαθήματος αυτού είναι να ρωτάτε εσείς διάφορα πράγματα που δεν έχετε καταλάβει σχετικά με τις ασκήσεις
που λύσαμε κατά τη διάρκεια του εξαμήνου. Να έρθετε λοιπόν καλά προετοιμασμένοι με τις ερωτήσεις σας.
Το τελικό διαγώνισμα είναι εδώ
και οι τελικοί βαθμοί εδώ.
Mihalis Kolountzakis
2017-01-25
![]() με
ζητούμενες ιδιότητες σύγκλισης (π.χ. κατά σημείο και όχι ομοιόμορφα).
με
ζητούμενες ιδιότητες σύγκλισης (π.χ. κατά σημείο και όχι ομοιόμορφα).
![]() , βαθμού το πολύ
, βαθμού το πολύ ![]() , το οποίο να παίρνει τη δεδομένη τιμή
, το οποίο να παίρνει τη δεδομένη τιμή ![]() στο σημείο
στο σημείο ![]() ,
για
,
για
![]() . (Τα σημεία
. (Τα σημεία ![]() υποτίθενται διαφορετικά ανά δύο.) Είδαμε πώς να το κάνουμε αυτό με γραμμική άλγεβρα αλλά και τα
πολυώνυμα Lagrange που δίνουν μια γρήγορη λύση σε αυτό το πρόβλημα.
υποτίθενται διαφορετικά ανά δύο.) Είδαμε πώς να το κάνουμε αυτό με γραμμική άλγεβρα αλλά και τα
πολυώνυμα Lagrange που δίνουν μια γρήγορη λύση σε αυτό το πρόβλημα.
![]() σε ένα σημείο
σε ένα σημείο ![]() κάνοντας μόνο
κάνοντας μόνο ![]() πολλαπλασιασμούς
και
πολλαπλασιασμούς
και ![]() προσθέσεις (εξοικονομώντας έτσι περίπου τους μισούς πολλαπλασιασμούς από τον υπολογισμό με την προφανή μέθοδο που προκύπτει από
τηα γραφή του πολυωνύμου ως άθροισμα μονονύμων).
προσθέσεις (εξοικονομώντας έτσι περίπου τους μισούς πολλαπλασιασμούς από τον υπολογισμό με την προφανή μέθοδο που προκύπτει από
τηα γραφή του πολυωνύμου ως άθροισμα μονονύμων).
![]() (και δε μπορεί δηλ. να πάρει οσοδήποτε μικρές θετικές τιμές). Πήραμε ως πρόβλημα στο σπίτι το να βρούμε ένα πολυώνυμο
(και δε μπορεί δηλ. να πάρει οσοδήποτε μικρές θετικές τιμές). Πήραμε ως πρόβλημα στο σπίτι το να βρούμε ένα πολυώνυμο ![]() δύο πραγματικών
μεταβλητών που είναι μεν πάντα θετικό αλλά μπορεί να πάρει οσοδήποτε μικρές θετικές τιμές.
δύο πραγματικών
μεταβλητών που είναι μεν πάντα θετικό αλλά μπορεί να πάρει οσοδήποτε μικρές θετικές τιμές.
![]() , τέτοιο ώστε (α)
, τέτοιο ώστε (α)
![]() , αλλά και
(β)
, αλλά και
(β)
![]() Με άλλα λόγια το πολυώνυμο
Με άλλα λόγια το πολυώνυμο ![]() είναι μεν πάντα θετικό αλλά μπορεί
να πάρει οσοδήποτε μικρές τιμές. Αυτό το φαινόμενο δε μπορεί να υπάρξει με πολυώνυμα μιας μεταβλητής. Αν ένα πολυώνυμο
είναι μεν πάντα θετικό αλλά μπορεί
να πάρει οσοδήποτε μικρές τιμές. Αυτό το φαινόμενο δε μπορεί να υπάρξει με πολυώνυμα μιας μεταβλητής. Αν ένα πολυώνυμο ![]() είναι πάντα θετικό τότε υπάρχει μια θετική σταθερά
είναι πάντα θετικό τότε υπάρχει μια θετική σταθερά ![]() τέτοια ώστε
τέτοια ώστε
![]() .
Ένα πολυώνυμο που έχει αυτές τις ιδιότητες είναι π.χ. το
.
Ένα πολυώνυμο που έχει αυτές τις ιδιότητες είναι π.χ. το
![]() .
.