Είναι τώρα εύκολο να δείξουμε ότι και η γλώσσα
![]() είναι
κανονική. Αρκεί να δείξουμε ότι το συμπλήρωμά της είναι, αλλά
είναι
κανονική. Αρκεί να δείξουμε ότι το συμπλήρωμά της είναι, αλλά
Έχοντας μια αντικατάσταση
![]() μπορούμε να
επεκτείνουμε το πεδίο ορισμού της από γράμματα του
μπορούμε να
επεκτείνουμε το πεδίο ορισμού της από γράμματα του ![]() σε λέξεις του
σε λέξεις του ![]() .
Αν
.
Αν
![]() ,
,
![]() , είναι
μια λέξη, τότε ορίζουμε (χρησιμοποιούμε το ίδιο σύμβολο
, είναι
μια λέξη, τότε ορίζουμε (χρησιμοποιούμε το ίδιο σύμβολο ![]() για να συμβολίσουμε
και την επεκτεταμένη συνάρτηση)
για να συμβολίσουμε
και την επεκτεταμένη συνάρτηση)
Αν ![]() είναι μια γλώσσα ορίζουμε ως συνήθως
είναι μια γλώσσα ορίζουμε ως συνήθως
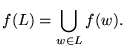
Επειδή κάθε πεπερασμένο σύνολο λέξεων είναι κανονική γλώσσα (γιατί;) από το προηγούμενο θεώρημα έπεται ότι οι ομομορφισμοί διατηρούν την κανονικότητα των γλωσσών.
Υπάρχουν γλώσσες που δεν είναι κανονικές. Αυτό είναι προφανές για πολύ γενικούς λόγους, που δεν έχουν τόσο πολύ να κάνουν με τη φύση των κανονικών γλωσσών, παρά μόνο με το γεγονός ότι κάθε κανονική γλώσσα επιδέχεται μια πεπερασμένη περιγραφή. Αυτή μπορεί να είναι είτε μια κανονική έκφραση, είτε η δομή ενός DFA που την αναγνωρίζει, για παράδειγμα.
Πόσες όμως διαφορετικές πεπερασμένες περιγραφές υπάρχουν;
Είναι φανερό ότι αυτές είνάι άπειρες το πλήθος (αφού π.χ. υπάρχουν οσοδήποτε μεγάλες κανονικές εκφράσεις), αλλά αυτό δεν είναι επαρκής πληροφορία για το πλήθος τους. Είναι πολύ πιο ακριβές το ότι υπάρχουν αριθμήσιμες το πλήθος πεπερασμένες περιγραφές, μπορούν δηλ. όλες οι πεπερασμένες περιγραφές να απαριθμηθούν: η περιγραφή 1, η περιγραφή 2, ..., η περιγραφή Ν, ..., με τρόπο ώστε να μη μείνει καμιά περιγραφή απ' έξω. Αυτός είναι ο ορισμός ενός αριθμήσιμου συνόλου. Ένα σύνολο δηλ. λέγεται αριθμήσιμο αν υπάρχει μια 1-1 απεικόνιση του συνόλου αυτού στους φυσικούς αριθμούς (βεβαιωθείτε ότι το καταλαβαίνετε αυτό).
Το γιατί το σύνολο όλων των πεπερασμένων εκφράσεων (πάνω από ένα σταθερό αλφάβητο ![]() )
είναι αριθμήσιμο είναι απλό. Αφού το
)
είναι αριθμήσιμο είναι απλό. Αφού το ![]() είναι πεπερασμένο υπάρχουν πεπερασμένο το πλήθος
εκφράσεις που μπορούν να φτιάξουμε με μήκος
είναι πεπερασμένο υπάρχουν πεπερασμένο το πλήθος
εκφράσεις που μπορούν να φτιάξουμε με μήκος ![]() , για κάθε
, για κάθε ![]() . Για την ακρίβεια, υπάρχουν
το πολύ
. Για την ακρίβεια, υπάρχουν
το πολύ
![]() τέτοιες εκφράσεις. Για να απαριθμήσουμε λοιπόν το σύνολο όλων
των πεπερασμένων εκφράσεων, αριθμούμε πρώτα τις εκφράσεις μήκους 1, μετά αυτές μήκους 2,
και συνεχίζουμε κατ' αυτόν τον τρόπο, ώστε δε μένει τίποτα αμέτρητο.
τέτοιες εκφράσεις. Για να απαριθμήσουμε λοιπόν το σύνολο όλων
των πεπερασμένων εκφράσεων, αριθμούμε πρώτα τις εκφράσεις μήκους 1, μετά αυτές μήκους 2,
και συνεχίζουμε κατ' αυτόν τον τρόπο, ώστε δε μένει τίποτα αμέτρητο.
Είναι αρκετά πιο δύσκολο (και παραλείπουμε την απόδειξη) να δούμε ότι το σύνολο
όλων των υποσυνόλων οποιουδήποτε άπειρου συνόλου δεν είναι αριθμήσιμο.
Έτσι, το σύνολο όλων των γλωσσών πάνω από το ![]() , δηλ. το σύνολο όλων των
υποσυνόλων του άπειρου συνόλου
, δηλ. το σύνολο όλων των
υποσυνόλων του άπειρου συνόλου ![]() δεν είναι αριθμήσιμο. Άρα υπάρχει κάποια γλώσσα
που δεν έχει αντίστοιχη πεπερασμένη περιγραφή, οπότε δεν είναι κανονική.
δεν είναι αριθμήσιμο. Άρα υπάρχει κάποια γλώσσα
που δεν έχει αντίστοιχη πεπερασμένη περιγραφή, οπότε δεν είναι κανονική.
Το παραπάνω είναι ένα πολύ γενικό επιχείρημα, όπως είπαμε, και δεν εξαρτάται σχεδόν καθόλου
από το τι εννοούμε κανονική γλώσσα, παρά μόνο ότι, ό,τι κι αν εννοούμε, η κανονική
γλώσσα μπορεί να περιγραφεί πλήρως με μια πεπερασμένη ακολουθία από γράμματα, διαλεγμένα από
ένα πεπερασμένο αλφάβητο. Με τον ίδιο τρόπο φαίνεται, π.χ. ότι υπάρχουν συναρτήσεις
![]() που δεν είναι υπολογίσιμες από πρόγραμμα, ουσιαστικά ότι κι αν εννούμε με αυτό.
Ας πούμε για παράδειγμα ότι θεωρούμε μια τέτοια συνάρτηση υπολογίσιμη αν υπάρχει ένα πρόγραμμα
σε κάποια γλώσσα προγραμματισμού, ας πούμε την C που υπολογίζει τη συνάρτηση αυτή.
Μα ένα πρόγραμμα αποτελεί πεπερασμένη περιγραφή της συνάρτησης, άρα, επειδή το πλήθος των συναρτήσεων
που δεν είναι υπολογίσιμες από πρόγραμμα, ουσιαστικά ότι κι αν εννούμε με αυτό.
Ας πούμε για παράδειγμα ότι θεωρούμε μια τέτοια συνάρτηση υπολογίσιμη αν υπάρχει ένα πρόγραμμα
σε κάποια γλώσσα προγραμματισμού, ας πούμε την C που υπολογίζει τη συνάρτηση αυτή.
Μα ένα πρόγραμμα αποτελεί πεπερασμένη περιγραφή της συνάρτησης, άρα, επειδή το πλήθος των συναρτήσεων
![]() δεν είναι αριθμήσιμο, υπάρχει κάποια στην οποία δεν αντιστοιχεί πρόγραμμα, που
δεν είναι δηλ. υπολογίσιμη.
δεν είναι αριθμήσιμο, υπάρχει κάποια στην οποία δεν αντιστοιχεί πρόγραμμα, που
δεν είναι δηλ. υπολογίσιμη.
Δε βοηθάει όμως αυτό το επιχείρημα στο να αποδείξει κανείς ότι συγκεκριμένες γλώσσες δεν είναι κανονικές. Αν και γνωρίζουμε δηλ. ότι οι περισσότερες γλώσσες (υπό μία έννοια) δεν είναι κανονικές, είναι παρ' όλα αυτά δύσκολο να δείξουμε αυτό για μια συγκεκριμένη γλώσσα που μας δίδεται, π.χ. για την
Είναι δύσκολο να μετατρέψουμε το παραπάνω διαισθητικό επιχείρημα σε απόδειξη, οπότε η μέθοδος
που ακολουθούμε για να δείξουμ εότι η ![]() δενείναι κανονική είναι αρκετά διαφορετική.
Χρησιμοποιούμε το ακόλουθο πολύ χρήσιμο λήμμα.
δενείναι κανονική είναι αρκετά διαφορετική.
Χρησιμοποιούμε το ακόλουθο πολύ χρήσιμο λήμμα.
Είναι φανερό ότι
![]() και ότι
και ότι
![]() , αφού σίγουρα όταν θα
έχουμε διαβάσει το
, αφού σίγουρα όταν θα
έχουμε διαβάσει το ![]() -οστό γράμμα της
-οστό γράμμα της ![]() θα έχουμε ήδη δεί τουλάχιστον μια κορυφή δύο φορές,
και ανάμεσα σε αυτές που έχουμε δεί δύο φορές η πρώτη είναι εξ ορισμού η
θα έχουμε ήδη δεί τουλάχιστον μια κορυφή δύο φορές,
και ανάμεσα σε αυτές που έχουμε δεί δύο φορές η πρώτη είναι εξ ορισμού η ![]() .
Επίσης είναι φανερό ότι το βρόγχο που ξεκινά και τελειώνει στην
.
Επίσης είναι φανερό ότι το βρόγχο που ξεκινά και τελειώνει στην ![]() μπορούμε να μην
το διανύσουμε καθόλου (οπότε δείχνουμε ότι η λέξη
μπορούμε να μην
το διανύσουμε καθόλου (οπότε δείχνουμε ότι η λέξη ![]() ) ή να τον διανύσουμε όσες
φορές θέλουμε, ας πούμε
) ή να τον διανύσουμε όσες
φορές θέλουμε, ας πούμε ![]() . Άρα η λέξη
. Άρα η λέξη
![]() , όπως οφείλαμε να δείξουμε.
, όπως οφείλαμε να δείξουμε.
![]()
Πώς χρησιμοποιούμε το Λήμμα Άντλησης για να δείξουμε ότι η γλώσσα ![]() δεν είναι κανονική; Υποθέτουμε ότι είναι και καταλήγουμε σε άτοπο.
Αν είναι λοιπόν, υπάρχει, από το Λήμμα Άντλησης, ένας φυσικός αριθμός
δεν είναι κανονική; Υποθέτουμε ότι είναι και καταλήγουμε σε άτοπο.
Αν είναι λοιπόν, υπάρχει, από το Λήμμα Άντλησης, ένας φυσικός αριθμός ![]() ,
τέτοις ώστε αν
,
τέτοις ώστε αν ![]() και
και
![]() τότε ισχύουν τα συμπεράσματα του
Λήμματος. Έχουμε
τότε ισχύουν τα συμπεράσματα του
Λήμματος. Έχουμε
![]() και
και
![]() ,
άρα
,
άρα ![]() , με
, με
![]() και μη κενό
και μη κενό ![]() , τέτοια ώστε για κάθε
, τέτοια ώστε για κάθε
![]() έχουμε
έχουμε
![]() .
Αυτό όμως δε γίνεται μια και η λέξη
.
Αυτό όμως δε γίνεται μια και η λέξη
![]() έχει σίγουρα περισσότερα 0 απ' ότι
1, αφού, λόγω του ότι
έχει σίγουρα περισσότερα 0 απ' ότι
1, αφού, λόγω του ότι
![]() , και το
, και το ![]() και το
και το ![]() έχουν μόνο μηδενικά
μέσα τους.
έχουν μόνο μηδενικά
μέσα τους.
Ας δούμε τώρα άλλη μια εφαρμογή του λήμματος άντλησης σε παρόμοιο πρόβλημα.
Για κάθε λέξη
![]() ,
,
![]() ,
ορίζουμε την αντεστραμμένη λέξη
,
ορίζουμε την αντεστραμμένη λέξη
![]() , να είναι
η
, να είναι
η ![]() με αντεστραμμένη τη σειρά των γραμμάτων του.
Ορίζουμε τη γλώσσα
με αντεστραμμένη τη σειρά των γραμμάτων του.
Ορίζουμε τη γλώσσα
Δείχνουμε τώρα ότι η ![]() δεν είναι κανονική.
Έστω ότι είναι και έστω
δεν είναι κανονική.
Έστω ότι είναι και έστω ![]() ο φυσικός αριθμός του οποίου η ύπαρξη
προκύπτει από το Λήμμα Άντλησης.
Ορίζουμε τη λέξη
ο φυσικός αριθμός του οποίου η ύπαρξη
προκύπτει από το Λήμμα Άντλησης.
Ορίζουμε τη λέξη
![]() που είναι στην
που είναι στην ![]() .
Γράφεται τότε η
.
Γράφεται τότε η ![]() ως
ως ![]() , με μη κενό
, με μη κενό ![]() και
και
![]() ,
οπότε και οι λέξεις
,
οπότε και οι λέξεις ![]() ,
, ![]() έχουν μέσα μόνο 1, ώστε
έχουν μέσα μόνο 1, ώστε
![]() ,
για
,
για
![]() .
Αλλά προφανώς η λέξη
.
Αλλά προφανώς η λέξη
![]() αφού αφαιρώντας το
αφού αφαιρώντας το ![]() αφαιρέσαμε κάποιους
άσσους από την αριστερή ομάδα άσσων αλλά όχι από τη δεξιά ομάδα, οπότε έχουμε
καταλήξει σε άτοπο, άρα η
αφαιρέσαμε κάποιους
άσσους από την αριστερή ομάδα άσσων αλλά όχι από τη δεξιά ομάδα, οπότε έχουμε
καταλήξει σε άτοπο, άρα η ![]() δεν είναι κανονική.
δεν είναι κανονική.