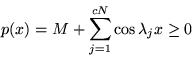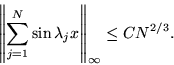- 1 Ωράριο
- 2 Περιγραφή του μαθήματος
- 3 Βαθμολογικό Σύστημα - Εξετάσεις
- 4 Ημερολόγιο Μαθήματος
- 4.1 Τρ, 12/2/02: Εισαγωγικά
- 4.2 1η εργασία
- 4.3 Τε, 13/2/02: Ανεξαρτησία,
 Νόμος Μεγάλων Αριθμών
Νόμος Μεγάλων Αριθμών
- 4.4 Τρ, 19/2/02: Εφαρμογές σε άλλους κλάδους των Μαθηματικών
- 4.5 Τε, 20/2/02: Το πρόβλημα του συλλέκτη κουπονιών. Ο Ασθενής Νόμος
των Μεγάλων αριθμών για
 ΤΜ
ΤΜ
- 4.6 2η εργασία
- 4.7 Τρ, 26/2/02: Το θεώρημα Borel-Cantelli
- 4.8 Πέ, 28/2/02: Βελτιωμένο Θ. Borel-Cantelli, μελέτη ακραίων τιμών
(record values)
- 4.9 3η εργασία
- 4.10 Πέ, 7/03/02: Record Values (ξανά) και Head Runs
- 4.11 4η εργασία
- 4.12 Τρ, 12/03/02: Ισχυρός νόμος μεγάλων αριθμών. Εφαρμογές.
- 4.13 Πέ, 14/03/02: Δεύτερη απόδειξη του Ισχυρού Νόμου με σύγκλιση σειρών
- 4.14 5η εργασία
- 4.15 Τρ, 19/3/02: Η ανισότητα Chernoff και εφαρμογές
- 4.16 6η εργασία
- 4.17 Πα, 22/3/02: Απόδειξη της ανισότητας Chernoff
- 4.18 Τρ, 26/3/02: Μετασχηματισμός Fourier σε
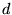 διαστάσεις
διαστάσεις
- 4.19 Πέ, 28/3/02: Αντιστροφή Μετασχ. Fourier
- 4.20 7η εργασία
- 4.21 Τρ, 1/4/02: Θεώρημα Helly για tight ακολουθίες μέτρων πιθανότητας
- 4.22 Πέ, 3/4/02: Θεώρημα συνέχειας του P. Levy
- 4.23 8η εργασία
- 4.24 Τρ, 9/4/02: Τέλος θεωρήματος συνέχειας. Κανονικές Τ.Μ.
- 4.25 Πα, 12/4/02: Ιδιότητες μέτρων Gauss.
- 4.26 Τρ, 16/4/02: Απόδειξη Κεντρικού Οριακού Θεωρήματος
- 4.27 Πέ, 18/4/02: Λύση ασκήσεων
- 4.28 9η εργασία
- 4.29 Τρ, 13/5/02: Εφαρμογές σε άλλους τομείς Μαθηματικών
- 4.30 Πέ, 15/5/02: Εφαρμογές σε άλλους τομείς Μαθηματικών
- 4.31 Τρ, 21/5/02: Εφαρμογές σε άλλους τομείς των Μαθηματικών
- 4.32 Πέ, 23/5/02: Εφαρμογές σε άλλους τομείς των Μαθηματικών
Αίθουσα Α 105. Τρ 9-11, Πέ 2-4.
Ώρες γραφείου: Τρ 11-13 (Η 304)
Σκοπός του μαθήματος αυτού είναι κυρίως η μελέτη Νόμων των
Μεγάλων Αριθμών (Laws of Large Numbers) και
Κεντρικών Οριακών Θεωρημάτων (Central Limit Theorems).
Γι'αυτά χρειάζεται αρκετά προχωρημένη ανάλυση η οποία θα αναπτυχθεί κατά
τη διάρκεια του μαθήματος. Υποτίθεται ότι οι ακροατές έχουν γνώση θεωρίας
μέτρου (όπως αυτή διδάσκεται στο μεταπτυχιακό μας πρόγραμμα). Αν αυτό δε συμβαίνει
για κάποιον, αυτός θα πρέπει (πράγμα όχι ακατόρθωτο) μέσα σε σύντομο
χρονικό διάστημα να αναπτύξει τουλάχιστον μια διαισθητική/φορμαλιστική κατανόηση
των εργαλείων της θεωρίας μέτρου (δηλ., ολοκλήρωση).
Το βιβλίο που θα χρησιμοποιηθεί κυρίως θα είναι το Probability: Theory and
Examples, 2η έκδοση, του R. Durrett.
Επίσης χρησιμοποιούμε το βιβλίο του K. Stromberg Probability for
Analysts.
Πέρα από τα θέματα που ανέφερα παραπάνω θα καταβάλω ιδιαίτερη προσπάθεια
να δείξω εφαρμογές της θεωρίας πιθανοτήτων, κυρίως στην Ανάλυση και τη
Συνδυαστική.
Γι' αυτά πιθανόν να χρησιμοποιηθούν άλλα βιβλία ή άρθρα.
Η αξιολόγηση των φοιτητών θα γίνει από (α) τη συμμετοχή τους στο μάθημα και
(β) από τη λύση ασκήσεων (θα δίδονται φυλλάδια ασκήσεων κάθε εβδομάδα).
Τελική γραπτή εξέταση θα γίνει μόνο εάν τα λυμμένα φυλλάδια ασκήσεων
δεν αντικατοπτρίζουν την πραγματική κατάσταση των φοιτητών.
Αναφερθήκαμε γρήγορα σε:
- Χώρους και μέτρα πιθανότητας
- Τυχαίες μεταβλητές με τιμές σε ένα χώρο που έχει σ-άλγεβρα (και ειδικότερα
στο
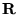 .
.
- Στο μέτρο (κατανομή) που επάγεται στο
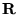 από μια ΤΜ
από μια ΤΜ
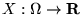 ,
καθώς και τη συνάρτηση κατανομής της
,
καθώς και τη συνάρτηση κατανομής της 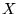 .
.
- Μέση τιμή της
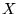 και της
και της 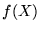 .
.
- Ανισότητες Jensen, Holder, Markov, Chebyshev
Λύστε τα θέματα του τελικού του προπτυχιακού μαθήματος Θ. Πιθανοτήτων
που βρίσκεται εδώ
Ορίσαμε τι σημαίνει ανεξαρτησία ενδεχομένων και επίσης τι σημαίνει ανεξαρτησία
μιας οικογένειας ΤΜ (αφού πρωτα ορίσαμε τι σημαίνει ανεξαρτησία μιας οικογένειας
από σ-άλγεβρες και ορίσαμε και τι είναι η σ-άλγεβρα μιας ΤΜ 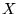 ).
).
Δείξαμε τον 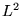 νόμο των μεγάλων αριθμών, ο οποίος είναι μια απλή συνέπεια
της ανισότητας Chebyshev. Ο νόμος αυτός λέει ότι αν έχουμε μια ακολουθία
ανά δύο ασυσχέτιστων ΤΜ
νόμο των μεγάλων αριθμών, ο οποίος είναι μια απλή συνέπεια
της ανισότητας Chebyshev. Ο νόμος αυτός λέει ότι αν έχουμε μια ακολουθία
ανά δύο ασυσχέτιστων ΤΜ 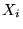 με κοινή μέση τιμή
με κοινή μέση τιμή 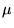 και
ομοιόμορφα φραγμένη διασπορά, και ορίσουμε
και
ομοιόμορφα φραγμένη διασπορά, και ορίσουμε
τότε η ΤΜ 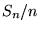 συγκλίνει στη σταθερά
συγκλίνει στη σταθερά 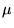 κατά
κατά 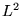 .
Δηλαδή
.
Δηλαδή
Η 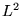 σύγκλιση συνεπάγεται και σύγκλιση κατά πιθανότητα, δηλ. για κάθε
σύγκλιση συνεπάγεται και σύγκλιση κατά πιθανότητα, δηλ. για κάθε 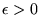
Σήμερα είδαμε μερικές εφαρμογές της Θ. Πιθανοτήτων σε διάφορους κλάδους
των Μαθηματικών. Αυτό είναι ένα θέμα που θα επανέρχεται κατά τη διάρκεια
του εξαμήνου και ελπίζω να δούμε εφαρμογές σε Θεωρία Αριθμών, Συνδυαστική,
Ανάλυση, Θεωρία Αλγορίθμων και αλλού.
Είδαμε σήμερα τα εξής.
- Χρησιμοποιήσαμε τις ιδιότητες της μέσης τιμής για να δείξουμε ότι
κάθε σύνολο
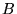 από
από 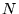 διαφορετικούς φυσικούς αριθμούς περιέχει ένα
υποσύνολο
διαφορετικούς φυσικούς αριθμούς περιέχει ένα
υποσύνολο 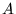 με μέγεθος τουλάχιστον
με μέγεθος τουλάχιστον 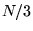 μέσα στο οποίο υποσύνολο
η εξίσωση
μέσα στο οποίο υποσύνολο
η εξίσωση 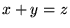 δεν έχει λύση. Τέτοια σύνολα ονομάζονται sum-free
και αυτό είναι ένα θεώρημα του Erdos.
δεν έχει λύση. Τέτοια σύνολα ονομάζονται sum-free
και αυτό είναι ένα θεώρημα του Erdos.
- Με ιδιότητες της μέσης τιμής μόνο επίσης δείξαμε ότι μπορεί κανείς να
χρωματίσει με δύο χρώματα τις ακμές του πλήρους γραφήματος με
 κορυφές
ώστε ο αριθμός των μονοχρωματικών τριγώνων που προκύπτουν να είναι το πολύ
κορυφές
ώστε ο αριθμός των μονοχρωματικών τριγώνων που προκύπτουν να είναι το πολύ
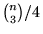 .
.
- Χρησιμοποιήσαμε τον ασθενή νόμο των μεγάλων αριθμών για να δείξουμε
το θεώρημα του Weierstrass(κάθε συνεχής συνάρτηση σε κλειστό διάστημα
προσεγγίζεται ομοιόμορφα από πολυώνυμα).
- Δείξαμε ότι για
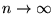 "τα περισσότερα" σημεία του κύβου
"τα περισσότερα" σημεία του κύβου
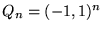 έχουν ευκλείδιο μήκος ανάμεσα σε
έχουν ευκλείδιο μήκος ανάμεσα σε
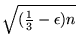 και
και
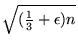 .
Τα περισσότερα (σε όγκο) δηλαδή σημεία του κύβου βρίσκονται συγκεντρωμένα
πολύ κοντά σε μια σφαίρα.
Και αυτό ήταν συνέπεια του ασθενή νόμου των μεγάλων αριθμών.
.
Τα περισσότερα (σε όγκο) δηλαδή σημεία του κύβου βρίσκονται συγκεντρωμένα
πολύ κοντά σε μια σφαίρα.
Και αυτό ήταν συνέπεια του ασθενή νόμου των μεγάλων αριθμών.
Σήμερα, την πρώτη ώρα, μελετήσαμε το εξής πρόβλημα. Τραβούμε από ένα δοχείο
με 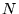 διαφορετικά αντικείμενα τυχαία ένα και το σημειώνουμε σ'ένα χαρτί. Μετά
το επανατοποθετούμε μέσα στο κουτί και συνεχίζουμε να επιλέγουμε και να σημειώνουμε
έως ότου έχουμε τραβήξει και τα
διαφορετικά αντικείμενα τυχαία ένα και το σημειώνουμε σ'ένα χαρτί. Μετά
το επανατοποθετούμε μέσα στο κουτί και συνεχίζουμε να επιλέγουμε και να σημειώνουμε
έως ότου έχουμε τραβήξει και τα 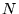 διαφορετικά αντικείμενα από μια φορά το καθένα
τουλάχιστον. Η ΤΜ που μας ενδιαφέρει εδώ είναι ο αριθμός των λήψεων που συμβαίνουν,
έστω
διαφορετικά αντικείμενα από μια φορά το καθένα
τουλάχιστον. Η ΤΜ που μας ενδιαφέρει εδώ είναι ο αριθμός των λήψεων που συμβαίνουν,
έστω 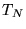 .
Είδαμε ότι
.
Είδαμε ότι
![${{\bf E}\left[{T_N}\right]} = N \sum_{k=1}^N {1\over k} \sim N \log N$](img27.png) και
επίσης εκτιμήσαμε και τη διασπορά του
και
επίσης εκτιμήσαμε και τη διασπορά του 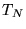 , πράγμα που μας επέτρεψε να δείξουμε
ότι
, πράγμα που μας επέτρεψε να δείξουμε
ότι
κατά πιθανότητα.
Τη δεύτερη ώρα δείξαμε τον εξής νόμο μεγάλων αριθμών: Αν
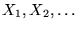 , είναι
ανεξάρτητες και ισόνομες με
, είναι
ανεξάρτητες και ισόνομες με
![${{\bf E}\left[{{\left\vert{X_i}\right\vert}}\right]}<\infty$](img30.png) , και
, και
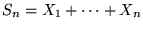 , τότε
, τότε
![$S_n / n \to \mu = {{\bf E}\left[{X_1}\right]}$](img32.png) κατά πιθανότητα.
κατά πιθανότητα.
Από σελ. 46 του βιβλίου λύστε τις 1-4, 7,8.
Την πρώτη ώρα είδαμε την εφαρμογή του Θ. 5.5 του βιβλίου στη μελέτη του
"προβλήματος του St. Petersburg". Αυτό είναι ένα παιχνίδι όπου η μέση
τιμή του αναμενόμενου κέρδους ανά παιχνίδι είναι άπειρη, πράγμα που δυσκολεύει
την εκτίμηση του πόσο πρέπει κανείς να πληρώσει για να παίξει αυτό το
παιχνίδι ώστε "να είναι τίμιο". Αυτό τώρα δεν μπορεί πλέον να ερμηνευτεί
ως ένα παιχνίδι του οποίου το κόστος είναι όσο και το μέσο κέρδος, για τον
απλούστατο λόγο ότι το μέσο κέρδος είναι άπειρο, αλλά δεν μπορεί φυσικά
το παιχνίδι αυτό να αποτιμηθεί ως άπειρο.
Η εναλλακτική λύση είναι να δείξουμε με χρήση του Θ. 5.5 ένα ασθενή νόμο
μεγάλων αριθμών της μορφής
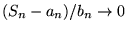 κατά πιθανότητα.
Η ποσότητα
κατά πιθανότητα.
Η ποσότητα 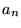 δηλώνει τότε πόσο πρέπει να πληρώσει κανείς για να παίξει
δηλώνει τότε πόσο πρέπει να πληρώσει κανείς για να παίξει
 παιχνίδια.
παιχνίδια.
Τη δεύτερη ώρα αποδείξαμε το Θ. Borel-Cantelli:
Θεώρημα 1 (α)
Αν
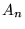
είναι μια ακολουθία από ενδεχόμενα με
![$\sum_n{{\bf {Pr}}\left[{A_n}\right]}<\infty$](img36.png)
τότε η πιθανότητα να ισχύουν άπειρα από τα
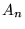
είναι 0.
(β) Αν
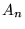
είναι μια ακολουθία από
ανεξάρτητα ενδεχόμενα με
![$\sum_n{{\bf {Pr}}\left[{A_n}\right]}=\infty$](img37.png)
τότε με πιθανότητα 1 ισχύουν άπειρα από αυτά.
Δείξαμε κατ' αρχήν το θεώρημα 6.7 που συνεπάγεται ότι η ύπαρξη πρώτης ροπής
(
![${{\bf E}\left[{{\left\vert{X}\right\vert}}\right]}<\infty$](img38.png) ) είναι αναγκαία συνθήκη για να έχουμε κάποιο
μεγάλων αριθμών.
) είναι αναγκαία συνθήκη για να έχουμε κάποιο
μεγάλων αριθμών.
Έπειτα δείξαμε το θεώρημα 6.8 που αποτελεί ένα βελτιωμένο και ποσοτικοποημένο
Θ. Borel-Cantelli.
Μελετήσαμε και το παράδειγμα 6.2 (record values). Προσέξτε γιατί στο βιβλίο
η αιτιολόγηση της ανεξαρτησίας είναι ανεπαρκής. Στο πρόβλημα αυτό κάνουμε
δειγματοληψία από ένα πληθυσμό (με συνεχή κατανομή) και τη χρονική
στιγμή
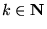 λέμε ότι έχουμε ρεκόρ αν
λέμε ότι έχουμε ρεκόρ αν 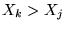 , για
, για
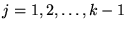 . Έστω
. Έστω 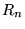 το πόσα ρεκόρ έχουμε για χρόνο μέχρι
το πόσα ρεκόρ έχουμε για χρόνο μέχρι  .
Κατ'αρχήν υπολογίζουμε
.
Κατ'αρχήν υπολογίζουμε
Έπειτα δείχνουμε (και αυτό έχει αρκετή δουλειά που το βιβλίο σας κάπως
θεωρεί προφανή) ότι τα ενδεχόμενα
είναι ανεξάρτητα.
Μετά από αυτό χρησιμοποιούμε το Θεώρημα 6.8 (βελτιωμένο Borel-Cantelli)
για να δείξουμε ότι
σχεδόν σίγουρα.
Από σελ. 52 ασκήσεις 6.7 και 6.8, και από σελ. 55 ασκήσεις 6.10 και 6.11.
Επαναλάβαμε τη μελέτη του προβλήματος για τα record values. Επίσης μελετήσαμε
το πρόβλημα για τα head runs: ρίχνουμε άπειρες φορές ένα τίμιο νόμισμα
και μελετάμε πόσο μεγάλο είναι το μέγιστο συνεχόμενο κομμάτι από κορώνες
στις  πρώτες ρίψεις. Δείξαμε ότι σχεδόν σίγουρα η ποσότητα αυτή είναι
ασυμπτοτική με
πρώτες ρίψεις. Δείξαμε ότι σχεδόν σίγουρα η ποσότητα αυτή είναι
ασυμπτοτική με 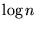 , δηλ. το πηλίκο αυτής και του
, δηλ. το πηλίκο αυτής και του 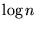 τείνει στο
1 για
τείνει στο
1 για 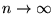 .
.
Από σελ. 55 ασκήσεις: 6.9, 6.13-16
Σήμερα είδαμε ότι με ακριβώς τις ίδιες προϋποθέσεις
(για την ακρίβεια, με ασθενέστερες προϋποθέσεις, μια και απαιτείται
μόνο ανεξαρτησία ανά δύο)
που είχαμε βάλει
για τον τελευταίο ασθενή νόμο που είχαμε δει, δηλ. ότι έχουμε
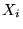 ανεξάρτητα ανά δύο και ισόνομα (iid), έχουμε
ανεξάρτητα ανά δύο και ισόνομα (iid), έχουμε
![${{\bf E}\left[{X_1}\right]} < \infty$](img47.png) και
και
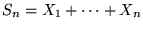 , έπεται ότι
, έπεται ότι
![$S_n /n \to {{\bf E}\left[{X_1}\right]}$](img48.png) ,
σχεδόν σίγουρα (και όχι μόνο κατά πιθανότητα, όπως είχαμε στον ασθενή νόμο).
,
σχεδόν σίγουρα (και όχι μόνο κατά πιθανότητα, όπως είχαμε στον ασθενή νόμο).
Να θυμίσουμε εδώ ότι σε χώρο μέτρου πεπερασμένο (όπως είναι οι χώροι πιθανοτήτων)
η σχεδόν παντού σύγκλιση συνεπάγεται σύγκλιση κατά μέτρο. Στην άλλη κατεύθυνση
το μόνο που μπορούμε να πούμε είναι ότι αν μια ακολουθία συναρτήσεων
συγκλίνει κατά μέτρο σε κάποιο όριο τότε υπάρχει μια υπακολουθία αυτής
που συγκλίνει σχεδόν παντού στο ίδιο όριο.
Με βάση αυτά που μόλις διαβάσατε δώστε προσοχή στην άσκηση 7.1 του βιβλίου σας
η οποία είναι λάθος.
Επίσης, η ανεξαρτησία που απαιτούνταν για τον ασθενή νόμο είναι ισχυρότερη
πρϋπόθεση απ΄ ό,τι απαιτείται - η ανεξαρτησία ανά δύο φτάνει για να δώσει
τον ισχυρό και συνεπώς και τον ασθενή νόμο.
Ως εφαρμογή νόμων ισχυρών αριθμών (όχι στην πραγματικότητα του τελευταίου
αυτού νόμου, αλλά άλλων ασθενέστερων που έχουμε δει πριν, όπως αυτού που
υποθέτει την ύπαρξη τέταρτης ροπής) είδαμε ότι σχεδόν όλοι οι πραγματικοί
αριθμοί είναι κανονικοί. Αυτό σημαίνει ότι για κάθε βάση αριθμητικού συστήματος
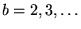 όλα τα δυνατά ψηφία
όλα τα δυνατά ψηφία
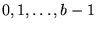 εμφανίζονται ασυμπτοτικά με
την ίδια συχνότητα στο
εμφανίζονται ασυμπτοτικά με
την ίδια συχνότητα στο 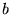 -αδικό ανάπτυγμα του αριθμού.
-αδικό ανάπτυγμα του αριθμού.
Επίσης είδαμε το θεώρημα Glivenko-Cantelli. Αν κάνουμε δειγματοληψία από ένα
οποιοδήποτε πληθυσμό (οποιαδήποτε δηλ. κατανομή 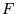 ) τότε σχεδόν σίγουρα η
εμπειρική συνάρτηση κατανομής
) τότε σχεδόν σίγουρα η
εμπειρική συνάρτηση κατανομής
συγκλίνει ομοιόμορφα στο 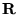 στην πραγματική συνάρτηση καανομής
στην πραγματική συνάρτηση καανομής 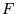 .
Κάναμε την απόδειξη μόνο όταν η
.
Κάναμε την απόδειξη μόνο όταν η 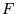 είναι συνεχής συνάρτηση, αλλά η ουσία δεν αλλάζει
ιδιαίτερα και στη γενική περίπτωση.
είναι συνεχής συνάρτηση, αλλά η ουσία δεν αλλάζει
ιδιαίτερα και στη γενική περίπτωση.
Σήμερα είδαμε κατ' αρχήν το 0-1 του Kolmogorov: Αν
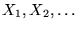 είναι
μια άπειρη ακολουθία ανεξαρτήτων ΤΜ και
είναι
μια άπειρη ακολουθία ανεξαρτήτων ΤΜ και 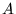 είναι ένα ενδεχόμενο που εξαρτάται
μόνο τελικά από τα
είναι ένα ενδεχόμενο που εξαρτάται
μόνο τελικά από τα 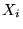 τότε οι μόνες δυνατές τιμές για το
τότε οι μόνες δυνατές τιμές για το
![${{\bf {Pr}}\left[{A}\right]}$](img54.png) είναι
0 ή 1. Για παράδειγμα, μια ακολουθία ανεξαρτήτων ΤΜ έχει όριο με πιθανότητα 0 ή 1,
δεν υπάρχουν άλλες δυνατές τιμές για αυτή την πιθανότητα.
Δεν δώσαμε αυστηρή απόδειξη του Θεωρήματος αυτού, αλλά περιγραψαμε τα βήματα που
απαιτούνται γι' αυτήν.
είναι
0 ή 1. Για παράδειγμα, μια ακολουθία ανεξαρτήτων ΤΜ έχει όριο με πιθανότητα 0 ή 1,
δεν υπάρχουν άλλες δυνατές τιμές για αυτή την πιθανότητα.
Δεν δώσαμε αυστηρή απόδειξη του Θεωρήματος αυτού, αλλά περιγραψαμε τα βήματα που
απαιτούνται γι' αυτήν.
Έπειτα είδαμε την ανισότητα Kolmogorov: Αν 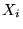 είναι ανεξάρτητες με μέση
τιμή 0 και πεπερασμένη δεύτερη ροπή τότε
είναι ανεξάρτητες με μέση
τιμή 0 και πεπερασμένη δεύτερη ροπή τότε
όου
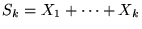 και
και 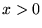 .
Η ανισότητα Chebyshev μας δίνει την ίδια ανισότητα αλλά μόνο για το τελεαταίο
άθροισμα
.
Η ανισότητα Chebyshev μας δίνει την ίδια ανισότητα αλλά μόνο για το τελεαταίο
άθροισμα 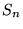 .
.
Χρησιμοποιήσαμε έπειτα την ανισότητα Kolmogorovγια να αποδείξουμε το κύριο
θεώρημα για τη σύγκλιση σειρών με ανεξάρτητους όρους: Αν 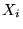 ανεξάρτητες με
μέση τιμή 0 και
ανεξάρτητες με
μέση τιμή 0 και
![$\sum_{n=1}^\infty {{\bf Var}\left[{X_n}\right]} < \infty$](img59.png) τότε η σειρά
τότε η σειρά
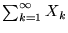 συγκλίνει σχεδόν σίγουρα.
συγκλίνει σχεδόν σίγουρα.
Αναφέραμε και το Θεώρημα Τριών Σειρών του Kolmogorov το οποίο δίνει τη
σύγκλιση τριών συγκεκριμένων σειρών ως αναγκαία και ικανή συνθήκη για τη σύγκλιση της σειράς
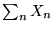 . Δείξαμε τη μία μόνο κατεύθυνση του θεωρήματος αυτού (που όμως δε
χρησιμοποιήσαμε σήμερα).
. Δείξαμε τη μία μόνο κατεύθυνση του θεωρήματος αυτού (που όμως δε
χρησιμοποιήσαμε σήμερα).
Πριν δώσουμε τη νέα απόδειξη του ισχυρού νόμου αποδείξαμε το λήμμα του Kronecker
Τέλος δώσαμε τη νέα απόδειξη του ισχυρού νόμου χρησιμοποιώντας αυτά που είδαμε σήμερα.
Επίσης δώσαμε την εξής, βελτιωμένη ποσοτικά, έκδοση του ισχυρού νόμου:
Αν 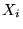 ανεξάρτητες και ισόνομες με μέση τιμή 0 και
ανεξάρτητες και ισόνομες με μέση τιμή 0 και
![${{\bf E}\left[{X_1^2}\right]} = \sigma^2 < \infty$](img63.png) ,
και
,
και
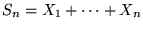 τότε, για κάθε
τότε, για κάθε 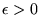 ,
,
σχεδόν σίγουρα.
Παρατηρείστε ότι η προηγούμενη μορφή του ισχυρού νόμου που είχαμε δεί είχε στον
παρανομαστή  αντί για
αντί για
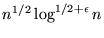 που έχουμε τώρα, άρα
η τωρινή μορφή είναι πολύ καλύτερη ποσοτικά.
που έχουμε τώρα, άρα
η τωρινή μορφή είναι πολύ καλύτερη ποσοτικά.
Ασκήσεις 7.3, 8.1, 8.3, 8.4 και 8.5
Διατυπώσαμε το ακόλουθο.
Θεώρημα 2 (Chernoff)
Αν
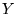
είναι άθροισμα ανεξαρτήτων 0-1 μεταβλητών και
![$\mu = {{\bf E}\left[{Y}\right]}$](img67.png)
τότε
![\begin{displaymath}
{{\bf {Pr}}\left[{{\left\vert{Y - \mu}\right\vert} > \epsilon\mu}\right]} < 2 e^{-c_\epsilon \mu},
\end{displaymath}](img68.png) |
(1) |
όπου
Παρατήρηση: Όταν
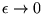 έχουμε
έχουμε
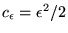 ενώ όταν
ενώ όταν
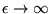 έχουμε
έχουμε
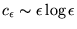 .
.
Το θεώρημα αυτό χρησιμοποιείται συχνότατα σε προβλήματα συνδυαστικής φύσης και
είναι τρομερά ευέλικτο. Δεν το αποδείξαμε αλλά είδαμε διάφορες εφαρμογές
του, μεταξύ των οποίων και το ακόλουθο θεώρημα του Erdos.
Θεώρημα 3 (Erdos, 1956)
Υπάρχει σύνολο θετικών ακεραίων
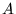
και σταθερές
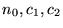
τέτοιες
ώστε
αν
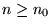
υπάρχουν τουλάχιστον
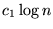
και το πολύ
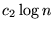
διαφορετικές αναπαραστάσεις του

ως άθροισμα δύο στοιχείων του
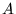
.
Γράψτε προσεκτικά και σε όλη της τη λεπτομέρεια την απόδειξη του παραπάνω θεωρήματος
του Erdos.
Αφιερώσαμε τη σημερινή μέρα στην απόδειξη της ανισότητας Chernoff.
Ακολουθήσαμε την απόδειξη στο βιβλίο "The Probabilistic Method"
των N. Alon και J. Spencer (Appendix).
Σήμερα ορίσαμε το μετασχηματισμό Fourier 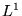 συναρτήσεων και ολικά
πεπερασμένων μέτρων στο
συναρτήσεων και ολικά
πεπερασμένων μέτρων στο 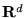 . Είδαμε ότι τα
. Είδαμε ότι τα 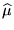 και
και 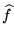 είναι ομοιόμορφα συνεχείς και φραγμένες συναρτήσεις και ότι (Riemann-Lebesgue)
είναι ομοιόμορφα συνεχείς και φραγμένες συναρτήσεις και ότι (Riemann-Lebesgue)
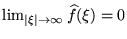 (το ίδιο δεν ισχύει για το
(το ίδιο δεν ισχύει για το
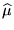 ).
).
Ορίσαμε τον πυρήνα του Gauss 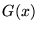 και υπολογίσαμε το μετασχηματισμό
Fourier του
και υπολογίσαμε το μετασχηματισμό
Fourier του
Ορίσαμε τη συνέλιξη 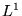 συναρτήσεων, μιας συνάρτησης κι ενός μέτρου καθώς
και δύο μέτρων και είδαμε τη βασική ανισότητα
συναρτήσεων, μιας συνάρτησης κι ενός μέτρου καθώς
και δύο μέτρων και είδαμε τη βασική ανισότητα
Από δω και πέρα θα ακολουθούμε το βιβλίο του K. Stromberg Probability
for Analysts.
Είδαμε ιδιότητες της συνέλιξης καθώς και τον ορισμό ασθενούς και ασθενούς *
σύγκλισης μέτρων. Είδαμε ότι η συνέλιξη με προσέγγιση της μονάδας συγκλίνει
(υπό διάφορες έννοιες) στο αντικείμενο που συνελίσσεται με την προσέγγιση
(Θ. 1.9). Μετά είδαμε πώς "αντιστρέφουμε" το μετασχ. Fourier με summability,
πράγμα το οποίο μας δίνει και τη μοναδικότητα του μετασχηματισμού.
Είδαμε τον τύπο αντιστροφής όταν και ο μετασχ. Fourier είναι ολοκληρώσιμος, καθώς
και τον έλεγχο του Dini, που μας δίνει ένα ικανό κριτήριο για να μπορούμε
να ανακασκευάσουμε την συνάρτση σε ένα σημείο γνωρίζοντας το μετασχ. Fourier της
συνάρτησης. Η αξία του κριτηρίου έγκειται στο ότι αναφέρεται μόνο στην ίδια τη
συνάρτηση, και όχι στο μετασχηματισμό της, όπως ο τύπος αντιστροφής (που απαιτεί
ο μετασχηματισμός να είναι ολοκληρώσιμος).
Από τη σελ. 14 του βιβλίου (Stromberg): 1-4, 6, 7, 10, 11.
Είδαμε σε ποιες περιπτώσεις μπορούμε να συνάγουμε ότι
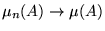 γνωρίζοντας ότι
γνωρίζοντας ότι 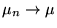 ασθενώς.
Ορίσαμε πότε μια ακολουθία
ασθενώς.
Ορίσαμε πότε μια ακολουθία 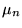 μέτρων πιθανότητας λέγεται tight (όταν
τα μέτρα έχουν μικρή μάζα έξω από μεγάλες σφαίρες ταυτόχρονα
για όλα τα
μέτρων πιθανότητας λέγεται tight (όταν
τα μέτρα έχουν μικρή μάζα έξω από μεγάλες σφαίρες ταυτόχρονα
για όλα τα  .
Τέλος είδαμε το θεώρημα του Helly: αν η ακολουθία μέτρων πιθανότητας
.
Τέλος είδαμε το θεώρημα του Helly: αν η ακολουθία μέτρων πιθανότητας
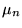 είναι tight τότε έχει ασθενώς συγκλίνουσα υπακολουθία.
είναι tight τότε έχει ασθενώς συγκλίνουσα υπακολουθία.
Να ξεκαθαρίσω εδώ ποια είναι η μορφή του θεωρήματος αναπαράστασης του
Riesz που χρησιμοποιήσαμε στις αποδείξεις: αν 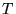 είναι ένα φραγμένο
γραμμικό συναρτησοειδές στο χώρο
είναι ένα φραγμένο
γραμμικό συναρτησοειδές στο χώρο
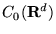 (ο οποίος έχει την ομοιόμορφη
νόρμα - προσέξτε, ο χώρος δεν είναι πλήρης) τότε υπάρχει ένα μέτρο
στο
(ο οποίος έχει την ομοιόμορφη
νόρμα - προσέξτε, ο χώρος δεν είναι πλήρης) τότε υπάρχει ένα μέτρο
στο 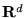 με φραγμένη ολική κύμανση τέτοιο ώστε για κάθε
με φραγμένη ολική κύμανση τέτοιο ώστε για κάθε
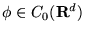 έχουμε
έχουμε
Επιπλέον, αν το 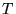 είναι μη αρνητικό (δηλ.
είναι μη αρνητικό (δηλ. 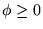 συνεπάγεται
συνεπάγεται 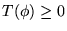 )
το μέτρο
)
το μέτρο 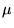 είναι μη αρνητικό.
είναι μη αρνητικό.
Σήμερα δείξαμε το κυριότερο μέρος του Θ. συνέχειας του P. Levy.
Δείξαμε ότι αν τα 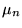 είναι μέτρα πιθανότητας στο
είναι μέτρα πιθανότητας στο 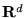 και
και
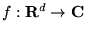 τ.ώ.
τ.ώ.
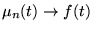 για
για
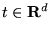 , τότε
αν
, τότε
αν 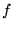 συνεχής στο 0 η ακολουθία
συνεχής στο 0 η ακολουθία 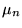 είναι tight.
είναι tight.
Για την απόδειξη χρησιμοποιήσαμε φυσικά ανάλυση Fourier. Εισαγάγαμε τον
πυρήνα του Fejer
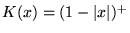 ο οποίος έχει τη σημαντική ιδιότητα
να έχει μη αρνητικό
ο οποίος έχει τη σημαντική ιδιότητα
να έχει μη αρνητικό 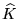 . Εκτιμήσαμε τη μάζα του μέτρου
. Εκτιμήσαμε τη μάζα του μέτρου 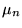 πάνω σε ένα διάστημα
πάνω σε ένα διάστημα 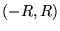 (κάναμε την απόδειξη μόνο στη μία διάσταση-δεν αλλάζει
σχεδόν τίποτα στις πολλές) προς τα κάτω από την ποσότητα
(κάναμε την απόδειξη μόνο στη μία διάσταση-δεν αλλάζει
σχεδόν τίποτα στις πολλές) προς τα κάτω από την ποσότητα
.
Αυτή την ποσότητα την εκτιμήσαμε χρησιμοποιώντας δυϊσμό, δηλ. την ταυτότητα
Από τη σελ. 26 του βιβλίου (Stromberg): 2, 3, 4, 6, 7, 9.
Τελειώσαμε την απόδειξη του Θ. συνέχειας του Levy. Είδαμε ότι αυτό
συνεπάγεται ότι αν έχουμε μέτρα πιθανότητας που συγκλίνουν κατά σημείο
σε κάποιο άλλο μέτρο πιθανότητας, τότε συγκλίνουν σε αυτό ομοιόμορφα
στα συμπαγή του 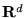 και ασθενώς.
και ασθενώς.
Αρχίσαμε να συζητάμε για τις αλγεβρικές κυρίως ιδιότητες των κανονικών
μέτρων πιθανότητας.
Τελειώσαμε σήμερα τη συζήτηση των ιδιοτήτων των ΤΜ με κανονική κατανομή.
Είδαμε ότι αυτές χαρακτηρίζονται από τη χαρακτηριστική τους συνάρτηση
(μετασχηματισμό Fourier της κατανομής τους) η οποία πρέπει να είναι της
μορφής
όπου 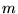 είναι η μέση τιμή του τυχαίου διανύσματος
είναι η μέση τιμή του τυχαίου διανύσματος 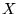 και
και 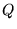 είναι
μια θετικά ημιορισμένη τετραγωνική μορφή.
είναι
μια θετικά ημιορισμένη τετραγωνική μορφή.
Σήμερα δείξαμε πώς μπορούμε να υπολογίσουμε τις παραγώγους της
χαρακτηριστικής συνάρτησης
![$f(t) = {{\bf E}\left[{e^{itX}}\right]}$](img106.png) μιας ΤΜ
μιας ΤΜ 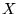 μέσω
των ροπών της
μέσω
των ροπών της 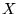 (για τιμές της παραγώγου στο
(για τιμές της παραγώγου στο 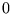 ).
).
Χρησιμοποιήσαμε αυτό για να δείξουμε το Κεντρικό Οριακό Θεώρημα
Lindeberg-Levy.
Σήμερα ασχοληθήκαμε με λύση ασκήσεων κατά τη διάρκεια του μαθήματος (αυτές
της σελίδας 14 του βιβλίου).
Από τη σελ. 106 του βιβλίου (Stromberg): 1, 2, 3, 14, 17, 18, 20, 22.
Ένα σύνολο
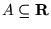 λέγεται universal in measure αν για κάθε
σύνολο
λέγεται universal in measure αν για κάθε
σύνολο
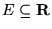 με θετικό μέτρο υπάρχει ένα
με θετικό μέτρο υπάρχει ένα
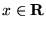 και
και 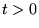 τέτοια ώστε
τέτοια ώστε
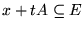 .
Υπάρχει δηλαδή ένα τουλάχιστον αφφινικό αντίγραφο του
.
Υπάρχει δηλαδή ένα τουλάχιστον αφφινικό αντίγραφο του 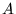 μέσα σε κάθε σύνολο
θετικού μέτρου.
μέσα σε κάθε σύνολο
θετικού μέτρου.
Κοιτώντας στη γειτονιά ενός σημείου πυκνότητας ενός συνόλου 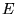 με θετικό μέτρο
έυκολα βλέπει κανείς πως όλα τα πεπερασμένα σύνολα είναι universal in measure.
Υπάρχει μια εικασία του Erdos που λέει ότι δεν υπάρχουν άπειρα σύνολα που
να είναι universal. Αυτή δεν έχει αποδειχθεί.
με θετικό μέτρο
έυκολα βλέπει κανείς πως όλα τα πεπερασμένα σύνολα είναι universal in measure.
Υπάρχει μια εικασία του Erdos που λέει ότι δεν υπάρχουν άπειρα σύνολα που
να είναι universal. Αυτή δεν έχει αποδειχθεί.
Δείξαμε σήμερα μια πιθανοθεωρητική κατασκευή, δεδομένου ενός άπειρου συνόλου 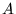 ,
που κατασκευάζει ένα σύνολο
,
που κατασκευάζει ένα σύνολο 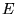 θετικού μέτρου τ.ώ.
το σύνολο
θετικού μέτρου τ.ώ.
το σύνολο
έχει (διδιάστατο) μέτρο μηδέν. Δοθέντος δηλαδή του 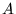 φτιάξαμε ένα σύνολο
φτιάξαμε ένα σύνολο
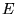 που δεν περιέχει σχεδόν κανένα αφφινικό αντίγραφο του
που δεν περιέχει σχεδόν κανένα αφφινικό αντίγραφο του 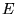 .
.
Μπορείτε να βρείτε τις λεπτομέρειες σε
αυτή εδώ την εργασία.
Δείξαμε κατ'αρχήν το ακόλουθο πολύ χρήσιμο θεώρημα:
Θεώρημα 4
Έστω
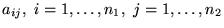
, πίνακας μιγαδικών αριθμών,
με
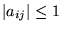
. Έστω επίσης
![$p_1,\ldots,p_{n_2} \in [0,1]$](img117.png)
και οι ΤΜ
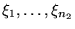
είναι ανεξάρτητες και
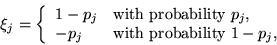 |
(2) |
Τότε, με πιθανότητα που τείνει στο 1 όταν
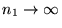
όπου
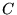
είναι μια απόλυτη σταθερά.
Χρησιμοποιώντας αυτό δείξαμε το ακόλουθο Θεώρημα
που αφορά σε τριγωνομετρικά πολυώνυμα:
Θεώρημα 5
(
Salemκαι
Zygmund)
Έστω
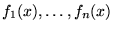
,
τριγωνομετρικά πολυώνυμα βαθμού το πολύ
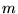
,
και
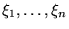
είναι
ανεξάρτητες ΤΜ
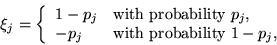 |
(3) |
για κάποια
![$p_j \in [0,1]$](img125.png)
.
Γράφουμε
Τότε, για κάποιο
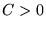
,
Χρησιμοποιήσαμε τέλος το Θεώρημα Salem- Zygmund για να δώσουμε
μια πιθανοθεωρητική κατασκευή για ένα τριγωνομετρικό πολυώνυμο
με 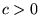 μια απόλυτη σταθερά, τα
μια απόλυτη σταθερά, τα 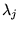 διαφορετικούς ακεραίους
και
διαφορετικούς ακεραίους
και
με 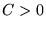 μια απόλυτη σταθερά.
μια απόλυτη σταθερά.
Περισσότερες λεπτομέρειες εδώ.
Σήμερα χρησιμοποιήσαμε μια παραλλαγή του Θ. Salem- Zygmundγια να
δείξουμε την εξής πρόταση:
Θεώρημα 6 (
Bourgain)
Υπάρχει απόλυτη σταθερά
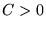
τέτοια ώστε για κάθε
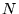
υπάρχουν θετικοί
διαφορετικοί ακέραιοι
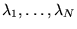
έτσι ώστε
Ή τετριμμένη άνω εκτίμηση είναι 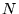 και η εκτίμηση που ισχύει από κάτω
είναι
και η εκτίμηση που ισχύει από κάτω
είναι 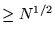 μια και η
μια και η 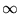 -νόρμα φράσσει την 2-νόρμα.
-νόρμα φράσσει την 2-νόρμα.
Δείξαμε σήμερα τη μέθοδο των πιθανοτήτων υπό συνθήκη (method of
conditional probabilities) για την άλγοριθμική κατασκευή αντικειμένων
των οποίων η ύπαρξη έχει αποδειχτεί πιθανοθεωρητικά.
Είναι μια πολύ γενικής εφαρμογής μέθοδος, και επιτρέπει πολλές
φορές να κατασκευάζει κανείς γρήγορα τα αντικείμενα αυτά.
Mihalis Kolountzakis
2002-05-24
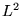 Νόμος Μεγάλων Αριθμών
Νόμος Μεγάλων Αριθμών
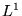 ΤΜ
ΤΜ
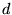 διαστάσεις
διαστάσεις
![\begin{displaymath}
{{\bf E}\left[{R_n}\right]} = \sum_{k=1}^n {1\over k} \sim \log n.
\end{displaymath}](img43.png)
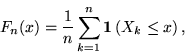
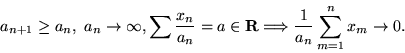
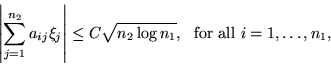
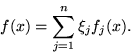
![\begin{displaymath}
{{\bf {Pr}}\left[{{\left\Vert{f}\right\Vert _\infty} \le
C ...
...log m\right)^{1/2}}\right]}
\to 1, \mbox{as $m\to\infty$}.
\end{displaymath}](img128.png)